Математическая модель нейрона

Приведем обобщенную математическую модель, в соответствии с которой нейрон представляет собой безынерционное устройство с n входными сигналами 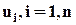и одним выходным сигналом у (рис. 3).

Рис. 3

Процесс преобразования входа включает в себя:

во-первых, вычисление функции передачи (функции распространения)

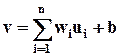, ( 1 )

представляющей собой взвешенную сумму всех входных сигналов, получаемых от нейронов-передатчиков, где весовые коэффициенты w_i, определяются синаптической силой соответствующих входным сигналам синапсов. Возбуждающим синапсам соответствуют положительные значения, а успокаивающим синапсам - отрицательные значения весовых коэффициентов. Величина v называется уровнем активации или внутренним входом нейрона. Чтобы учесть то обстоятельство, что уровень активации нейрона в отсутствие входных сигналов u_i не является нулевым, к взвешенной сумме добавляется так называемое смещение b;

во-вторых, так называемую активационную функцию (функцию активации f), преобразующую уровень активации v в выходной сигнал нейрона у. Для этой цели используются различные функции, среди которых наиболее распространенной является сигмоидальная функция (рис.4), описываемая следующим выражением

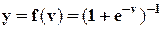(2)

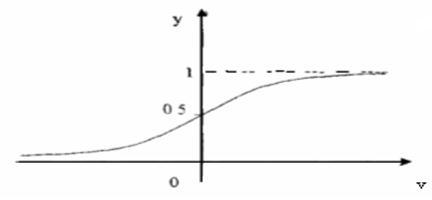
Рис.4

В этой функции при любых значениях v множество значений y ограничено интервалом [0,1]. Крутизна нелинейной характеристики нейрона

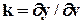
определяется производной от активационной функции.

Для сигмоидальной функции, описываемой (2), крутизна имеет вид

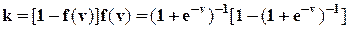(3)

и изменяется в зависимости от уровня активацииот малых значений (при отрицательных значениях v) до максимального значения (при нулевом уровне активации) и снова уменьшается при больших положительных значениях v.

Самой простой формой активационной функции является линейная функиия, описываемая выражением

y=kv, (4)

где k - некоторая постоянная. В ряде случаев ее принимают равной единице.

Для упрощения изображения нейрона (рис. 2) используем понятие узла, известное в сигнальных графах. При этом в случае двух входов нейрон можно представить графически в более простом виде (рис. 5).

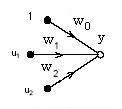
Рис. 5

На этом рисунке узел является графическим изображением двух операций, определяемых уравнениями (1) и (2), причем 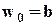. При этом

.

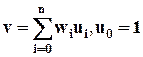Дата добавления: 2014-01-07