Многослойная нейронная сеть

Многослойная нейронная сеть включает в себя один или несколько скрытых слоев, нейроны которых называют скрытыми нейронами (рис. 1). Граф на рис. 6 изображает многослойную сеть с одним скрытым нейроном. Когда мы говорим, что сеть состоит из N слоев, мы учитываем лишь скрытые слои и выходной слой. Входной слой при этом не учитывается, т.к. его узлы не отражают никаких действий вычислительного характера. Однослойная нейронная сеть, таким образом, состоит из одного выходного слоя.

Рис. 6

Найдем математическую модель двухслойной сети, полагая, что в каждом слое используется одна и та же активационная функция (функция активации f) и что число входов n и число выходов m. Считаем, что скрытый слой содержит c нейронов. Для двухслойной нейронной сети, представленной на рис. 6, n = m =2, c =3. Ради простоты мы не показываем смещения нейронов.

В нейронах скрытого слоя, во-первых, вычисляется взвешенная сумма входных сигналов u₁ и u₂, так что внутренний сигнал i -го нейрона этого слоя определяется как

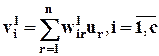. (4a)

Затем используется нелинейная активационная функция f,чтобы вычислитьвыходной сигнал i -го нейрона скрытого слоя

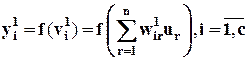. (4b)

Заметим, что активационные функции вводят в нейронную сеть нелинейности и при этом придают ей устойчивость в работе.

Выходной сигнал активационной функции в общем случае проходит непосредственно на выход i -го нейрона скрытого слоя (хотя имеются исключения, когда используется динамический фильтр), после чего он поступает на входы нейронов следующего слоя посредством весовых коэффициентов. Для двухслойной сети следующим слоем является выходной слой, так что внутренний сигнал j -го нейрона этого слоя определяется как

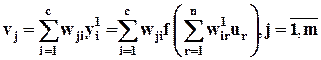. (4c)

Затем с помощью активационной функции выходного слоя окончательно формируется выходной сигнал j -го нейрона, другими словами, j -й выходной сигнал нейронной сети

. (4d)

Несмотря на простоту рассмотренной структуры, эта модель нейронной сети весьма универсальна. Показано, что нейронная сеть с одним скрытым слоем, может аппроксимировать любую непрерывную функцию с любой степенью точности (если имеется достаточное число нейронов в скрытом слое). Следует сказать, что нейронная сеть с двумя скрытыми слоями может аппроксимировать всецело любую функцию.

Различают два режима работы нейронной сети рабочий режим и режим обучения.

В рабочем режиме имеет место прямое распространение сигнала от входа к выходу. Хотя применяются нейронные сети с обратной связью, мы ограничимся лишь изучением многослойной сети с однонаправленным распространением входного сигнала (персептрона). В режиме обучения используется как прямое, так и обратное распространение сигнала, которое сводится к тому, что сигнал ошибки e=d-y=(e₁,…,e_m) между желаемым d=(d₁,…,d_m) и действительным y=(y₁,…,y_m) значениями выхода используется для подстройки весов и смещений выходного и скрытого слоев.

Дата добавления: 2014-01-07