
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Обратное распространение ошибки. Метод обратного распространения ошибки представляет собой популярную процедуру обучения многослойного персептрона
|
|
|
|
Лекция 25
Метод обратного распространения ошибки представляет собой популярную процедуру обучения многослойного персептрона. Он основан на дельта-правиле и использует критерий качества обучения (сумму квадратов ошибок ej=dj-yj)
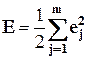 (5)
(5)
для нейронов выходного слоя. Этот критерий есть сумма квадратов ошибок, получаемых на выходе каждого нейрона выходного слоя.
Весовой коэффициент 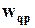 передачи сигнала от p -го нейрона предыдущего слоя к q -му нейрону последующего слоя обновляется в соответствии с обобщенным дельта-правилом
передачи сигнала от p -го нейрона предыдущего слоя к q -му нейрону последующего слоя обновляется в соответствии с обобщенным дельта-правилом
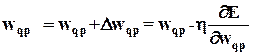 . (6)
. (6)
Чтобы обозначения были более понятными, мы опустили индекс обучающего образца k; очевидно, что уравнение (6) является рекуррентным, т.е. 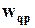 в его левой части представляет новое значение весового коэффициента, в то время как
в его левой части представляет новое значение весового коэффициента, в то время как 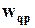 в правой части является прежним весом. Здесь
в правой части является прежним весом. Здесь 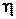 - параметр скорости обучения. В обобщенном дельта-правиле корректировка весового коэффициента
- параметр скорости обучения. В обобщенном дельта-правиле корректировка весового коэффициента  пропорциональна градиенту ошибки
пропорциональна градиенту ошибки 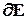 /
/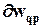 , другими словами, чувствительности критерия качества к изменению весового коэффициента. Чтобы применить данный алгоритм, необходимы два цикла вычислений, прямое распространение и обратное распространение.
, другими словами, чувствительности критерия качества к изменению весового коэффициента. Чтобы применить данный алгоритм, необходимы два цикла вычислений, прямое распространение и обратное распространение.
В прямом цикле вычислений веса остаются неизменными. Прямое распространение сигнала начинается в последнем скрытом слое, ведя счет от выходного слоя, путем подачи на его вход образцового входного векторного сигнала и заканчивается в выходном слое после вычисления сигнала ошибки (разности между образцовым выходным сигналом и выходным сигналом нейрона) для каждого нейрона выходного слоя. Обратное распространение сигнала начинается в выходном слое и продолжается путем распространения сигнала ошибки назад справа налево через всю сеть, слой за слоем.
Для описания алгоритма обратного распространения сигнала ошибки предположим, что j – й нейрон является нейроном выходного слоя (рис. 7). На рис. 7 показаны в явном виде связи между нейроном j выходного слоя, нейроном i скрытого слоя 1, нейроном r скрытого слоя 2 и нейроном s скрытого слоя 3.
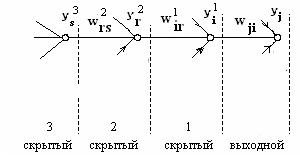
Рис. 7
Заменяя в 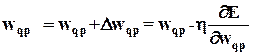 (6) q на j и p на i, получаем формулу для настройки весовых коэффициентов выходного слоя
(6) q на j и p на i, получаем формулу для настройки весовых коэффициентов выходного слоя
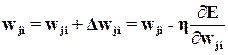 . (6а)
. (6а)
Используя цепное правило дифференцирования, запишем производную, входящую в уравнение (6а), в виде
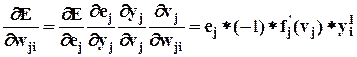 . (7)
. (7)
Здесь с учетом (5) 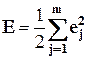
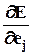 =
=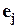 =
=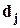 -
-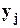
есть ошибка j- го нейрона, 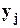 есть выход j- го нейрона,
есть выход j- го нейрона,
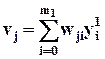
есть внутренний вход j- го нейрона, полученный на основании (4c) 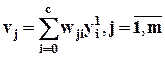 , после суммирования взвешенных выходов всех нейронов m1 предшествующего первого скрытого слоя, в том числе выхода
, после суммирования взвешенных выходов всех нейронов m1 предшествующего первого скрытого слоя, в том числе выхода 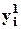 i -го нейрона этого слоя,
i -го нейрона этого слоя, 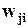 есть весовой коэффициент передачи сигнала от i -го нейрона первого скрытого слоя к входу j- го нейрона выходного слоя.
есть весовой коэффициент передачи сигнала от i -го нейрона первого скрытого слоя к входу j- го нейрона выходного слоя.
При этом
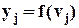 ,
,
где 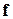 - активационная функция. Как
- активационная функция. Как 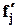 обозначена производная от функции
обозначена производная от функции 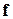 по ее аргументу. С учетом
по ее аргументу. С учетом 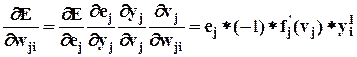 (7) и (4c) при c = m1, находим с помощью
(7) и (4c) при c = m1, находим с помощью 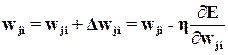 (6а)
(6а)
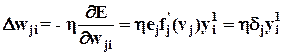 , (8)
, (8)
где
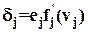 . (8a)
. (8a)
Как видим, для обновления весовых коэффициентов выходного слоя надо найти ошибку 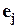 , выход
, выход 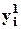 i -го первого скрытого слоя и производную
i -го первого скрытого слоя и производную 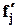 .
.

Найдем формулу для обновления коэффициентов первого скрытого слоя
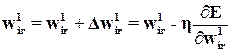 . (9)
. (9)
Ошибка 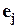 j -го нейрона выходного слоя связана с желаемым выходом
j -го нейрона выходного слоя связана с желаемым выходом 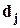 и очевидно, что
и очевидно, что 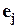 =
=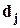 -
-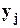 . Для i -го нейрона первого скрытого слоя в соответствии с методом обратного распространения ошибки мы должны использовать ошибку
. Для i -го нейрона первого скрытого слоя в соответствии с методом обратного распространения ошибки мы должны использовать ошибку 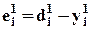 , т.к. она по аналогии с
, т.к. она по аналогии с 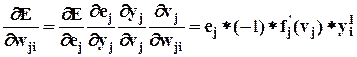 (7) должна входить в первые две частные производные для
(7) должна входить в первые две частные производные для 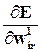 . Однако возникает проблема, обусловленная тем обстоятельством, что такая ошибка неизвестна для нейронов скрытого слоя. Чтобы преодолеть эту трудность, определим произведение упомянутых производных непосредственно
. Однако возникает проблема, обусловленная тем обстоятельством, что такая ошибка неизвестна для нейронов скрытого слоя. Чтобы преодолеть эту трудность, определим произведение упомянутых производных непосредственно
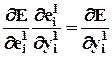 . (10)
. (10)
Частная производная от 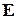 по выходу i -го нейрона первого скрытого слоя, с учетом
по выходу i -го нейрона первого скрытого слоя, с учетом 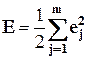 (5) прямо связанная с выходом j- го нейрона выходного слоя, определяется как
(5) прямо связанная с выходом j- го нейрона выходного слоя, определяется как
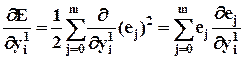 (11)
(11)
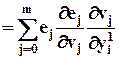
 (12)
(12)
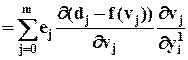 (13)
(13)
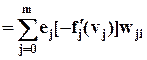 . (14)
. (14)
Для получения последнего результата принято во внимание, что в соответствии с (4с)
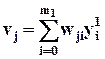 ,(4c)
,(4c)
где m1 число нейронов первого скрытого слоя.
Используя цепное правило дифференцирования с учетом  (14) и
(14) и
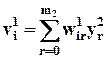 (17), где m2 число нейронов второго скрытого слоя, запишем
(17), где m2 число нейронов второго скрытого слоя, запишем
производную
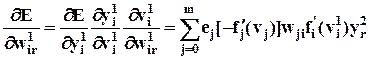 . (15)
. (15)
При этом c помощью дельта-правила 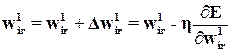 (9) и
(9) и 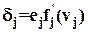 (8а) получаем формулу для обновления коэффициентов первого скрытого слоя
(8а) получаем формулу для обновления коэффициентов первого скрытого слоя
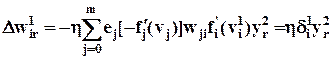 , (16)
, (16)
где
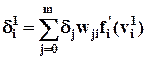 . (16а)
. (16а)
Здесь i – номер нейрона первого скрытого слоя, r – номер нейрона второго скрытого слоя, предшествующего первому скрытому слою (считая справа налево), j – номер нейрона выходного слоя. Множитель 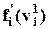 зависит лишь от активационной функции i –го нейрона первого скрытого слоя и
зависит лишь от активационной функции i –го нейрона первого скрытого слоя и 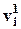 . Значения
. Значения 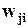 содержат весовые коэффициенты, связанные с нейронами выходного слоя. Наконец,
содержат весовые коэффициенты, связанные с нейронами выходного слоя. Наконец, 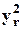 есть выход r –го нейрона второго скрытого слоя и этот выход появляется в выражении для
есть выход r –го нейрона второго скрытого слоя и этот выход появляется в выражении для 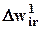 в результате вычисления производной
в результате вычисления производной
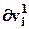 /
/ 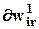 , т.к. внутренний вход i -го нейрона
, т.к. внутренний вход i -го нейрона 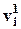 равен
равен
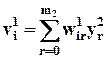 . (17)
. (17)
Как видим, операция суммирования по j требует знания ошибок для всех нейронов выходного слоя посредством 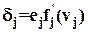 . Это говорит о том, что как бы ошибка
. Это говорит о том, что как бы ошибка 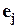 =
=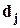 -
-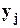 , имеющая место на выходе нейронной сети, «переместилась назад» с выходного слоя на первый скрытый слой.
, имеющая место на выходе нейронной сети, «переместилась назад» с выходного слоя на первый скрытый слой.

Для s -го нейрона следующего второго скрытого слоя, предшествующего первому скрытому слою, правило обновления применяется рекуррентно по аналогии с (16) и (16а):
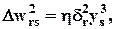
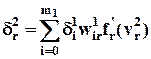 . (17а)
. (17а)
Здесь ошибка 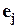 =
=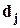 -
-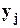 фигурирует в
фигурирует в 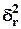 посредством
посредством 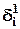 и теперь имеет место перемещение этой ошибки с первого скрытого слоя на второй скрытый
и теперь имеет место перемещение этой ошибки с первого скрытого слоя на второй скрытый
слой.
|
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 906; Нарушение авторских прав?; Мы поможем в написании вашей работы!