Лекция 26

В общем, коррекция (обновление) весового коэффициента 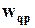, связывающего вход p –го нейрона данного слоя с выходом q – го нейрона предшествующего слоя, определяется как

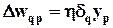. (18)

Здесь 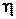- параметр скорости обучения, 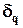- называется локальным градиентом [сравните с 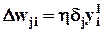(8), 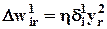(16) и (17а)] и 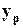- входной сигнал q –го нейрона.

Локальный градиент вычисляется рекуррентно для каждого нейрона и его выражение зависит от того, где расположен нейрон в выходном или скрытом слое:

1. Если q – й нейрон принадлежит выходному слою, то согласно (8а)

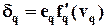. (19)

Оба сомножителя в произведении относятся к q –му нейрону.

2. Если q – й нейрон расположен в k –ом скрытом слое (рис. 8), то согласно 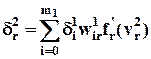(17а) при замене r на q, 2 на k, 1 на k - 1 и i на r,

получаем

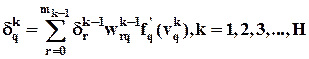, (20)

где H – число скрытых слоев в нейронной сети, m_k-1 -число нейронов (k - 1)-го скрытого слоя.

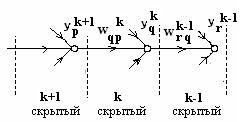
Рис. 8

Как видим, 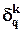представляет собой взвешенную сумму локальных градиентов 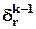нейронов, расположенных в (k - 1)-ом слое, непосредственно предшествующем k -омускрытому слою (считая, справа налево), причем 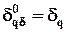и вычисляется по формуле (19), а 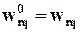, m₀=m. Так при k = 1 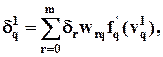что совпадает с (16а) при замене r на j и q на i.

Весовые коэффициенты связей, питающих выходной слой, обновляются за счет использования дельта-правила (18), в котором локальный градиент 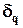определяется по выражению (19). Вычислив 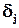для всех нейронов выходного слоя, мы затем используем (20), чтобы найти локальные градиенты для всех нейронов следующего слоя и изменить все весовые коэффициенты связей, питающих этот слой. Чтобы можно было вычислить 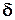для каждого нейрона, активационная функция 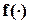всех нейронов должна быть дифференцируемой.

Алгоритм. Алгоритм обратного распространения включает пять шагов.

а) Инициализация весовых коэффициентов. Установите все весовые коэффициенты равными небольшим случайным числам.

б) Предъявление входов и соответствующих им желаемых выходов (обучающие пары). Подаем на нейронную сеть вектор входа u и соответствующий желаемый вектор выхода d. Вход может быть новым в каждой новой попытке обучения или образцы из обучающего множества могут подаваться на сеть циклически до тех пор, пока весовые коэффициенты не стабилизируются, т.е. перестанут изменяться.

в) Вычисление действительных значений выхода. Вычисляем вектор выхода последовательно используя выражение 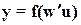, где f есть вектор активационных функций.

г) Настройка весовых коэффициентов. Начинаем настройку с весов выходного слоя и затем идем назад к последнему скрытому слою (считая справа налево). Весовые коэффициенты настраиваем с помощью

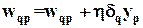. (21)

В этом уравнении 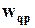есть весовой коэффициент соединения, связывающего нейрон p скрытого слоя с нейроном q следующего слоя, 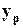- выход нейрона p (или внешний вход для нейрона q), 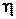есть параметр скорости обучения и 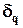- градиент. Если нейрон q является нейроном выходного слоя, то 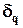вычисляется с помощью (19) 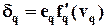и если нейрон q является нейроном скрытого слоя, то 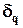определяется с помощью (20) 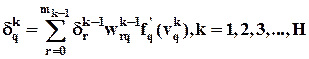. Ускорение сходимости можно иногда обеспечить, если добавить значение момента.

Замечание. Для пакетного режима обработки дельта-правило (6) 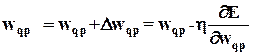модифицируется

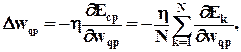
где 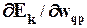вычисляется в режиме онлайн и затем накапливается в процессе представления обучающих данных для , как составная часть обратных вычислений. Как видим, весовые коэффициенты обновляются после представления всех обучающих данных. Алгоритм онлайн проще для реализации и требует меньше памяти, чем алгоритм офлайн. Однако алгоритм онлайн обеспечивает более точную оценку вектора градиента и более простую сходимость к локальному минимуму.

Пример (локальный градиент). Логистическая (сигмоидная) функция 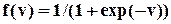дифференцируема, и ее производная имеет вид 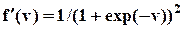. Мы можем исключить экспоненту и записать производную как

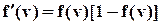. (22)

Для нейрона j в выходном слое мы можем выразить локальный градиент как

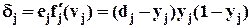. (23)

Для нейрона i скрытого слоялокальный градиент равен

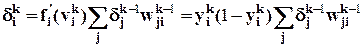. (24)

Пример (обратное распространение). Чтобыближе познакомиться с методом обратного распространения ошибки, рассмотрим простой пример с обучающим комплектом данных

Дата добавления: 2014-01-07