Алгоритм обучения ANFIS

Если параметры предпосылок фиксированы, то выход всей сети является линейной комбинацией параметров заключений. В символах этот выход может быть записан в виде

(7)

(8)

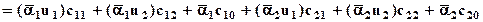(9)

и он представляет линейную комбинацию параметров заключений (i=1,2; j=0,1,2). Гибридный алгоритм настраивает параметры заключений при прямом распространении сигнала и параметры предпосылок

{ a_i, b_i, c_i } при обратном распространении сигнала. При прямом распространении сеть передает входные сигналы в прямом направлении до слоя 4, в котором параметры заключений идентифицируются с помощью метода наименьших квадратов или путем псевдоинверсии матрицы. При обратном распространении сигнал ошибки передается в обратном направлении, и параметры предпосылок обновляются с помощью метода обратного распространения ошибки.

В связи с тем, что обновления параметров предпосылок и заключений происходят раздельно, в гибридных обучающих алгоритмах можно ускорить процесс вычислений путем использования различных вариантов

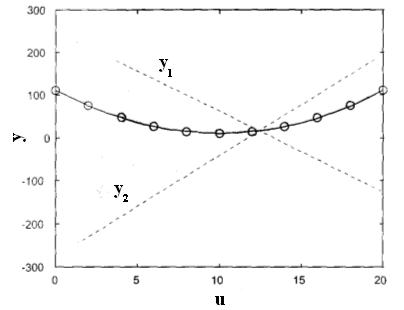
Рис. 2

градиентных методов или других методах оптимизации для настройки параметров предпосылок.

Пример (ANFIS). Посмотрим, как сеть может аппроксимировать нелинейную функцию. Рис. 2 показывает изображение множества данных и результирующую интерполирующую кривую. Одиннадцать точек данных (кружки на рисунке) были предъявлены сети ANFIS. В начале были

Рис. 2

выбраны параметры двух гауссовских функций принадлежности (рис. 3, слева). Они занимали весь универсум входа с 50 процентным перекрытием между собой. Другим выбором начального шага проектирования был выбор числа правил, т. е. двух правил. В результате обучения эти правила приняли следующий вид,

Если u есть A₁ то y₁ = -18,75 u + 249,1, (10)

Если u есть A₂ то y₂ = 23,55 u – 276,7. (11)

Правой стороне правил соответствуют две прямые линии, также нарисованные на рис. 2, одна из которых имеет положительный, а другая отрицательный наклон. Интерполирующая кривая является результатом нелинейной комбинации этих двух прямых. Вес значений прямых линий в каждой точке интерполяционной кривой определяется видом функций принадлежности входа (рис. 3, справа), который они приняли после обучения.

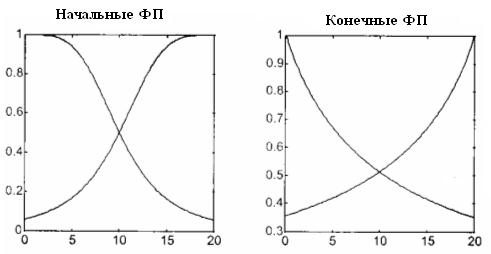
Рис. 3

Одиннадцать точек данных были предъявлены сети 100 раз и каждый раз алгоритм обучения ANFIS обновлял параметры предпосылок, что определило форму и положение двух функций принадлежности, и параметры заключений, что в свою очередь определило наклон и постоянные двух прямых линий, описываемых уравнениями в правой части правил. Начальные значения коэффициентов для этих уравнений были взяты равными нулю.

Дата добавления: 2014-01-07