Лекция 29

Генетические алгоритмы

Проблема использования для обучения сети алгоритма обратного распространения ошибки и оптимизации по методу наименьших квадратов состоит в том, что их применение может быть причиной останова оптимизационного процесса в точках локального минимума нелинейной целевой функции (критерия качества сети). Дело в том, что упомянутые методы основаны на вычислениях производных и являются градиентными методами. Генетические алгоритмы − естественный отбор самого подходящего (выживает наиболее приспособленный!) − не требуют вычисления производных и являются стохастическими оптимизационными методами, поэтому менее склонны к останову оптимизационного процесса в локальных минимумах. Эти алгоритмы могут быть использованы для оптимизации, как структуры, так и параметров в нейронных сетях. Специальная область их применения связана с определением параметров нечетких функций принадлежности.

Генетические алгоритмы имитируют естественную эволюцию популяций. Суть этих алгоритмов такова. В начале генерируют возможные различные решения, используя генератор случайных чисел. Затем происходит тестирование (оценка) этих возможных решений с точки зрения поставленной задачи оптимизации, т.е. определяется, насколько хорошее решение они обеспечивают. После чего часть лучших решений отбирается, а другие отсеваются (выживает наиболее приспособленный). Затем отобранные решения подвергаются процессам репродукции (размножения), скрещивания и мутации, чтобы создать новую генерацию (поколение, потомство) возможных решений, которая, как ожидаемо, будет более подходящей, чем предыдущая генерация. Наконец, создание и оценивание новых генераций продолжатся до тех пор, пока последующие поколения не будут давать более подходящих решений. Такой алгоритм поиска решений из широкого спектра возможных решений оказывается предпочтительнее с точки зрения окончательных результатов, чем обычно используемые алгоритмы. Платой является большой объем вычислений. Рассмотрим составные части генетического алгоритма.

1. Кодирование. Множество параметров для задачи оптимизации кодируется в последовательность бит. Например, точка с координатами (x,y)=(11, 6) может быть представлена как хромосома, которая имеет вид соединения двух битовых последовательностей

Каждая координата представлена геном из четырех бит. Могут быть использованы другие методы кодирования и могут быть предусмотрены меры для кодирования отрицательных чисел и чисел с плавающей запятой.

2. Вычисление функции приспособленности (соответствия). После генерации популяции хромосом вычисляется значение функции приспособленности (соответствия) для каждой из ее хромосом. Функция приспособленности определяется через целевую функцию путем ее инвертирования (целевая функция минимизируется, а функция приспособленности максимизируется). Для задач максимизации значение функции приспособленности i-го члена вычисляется как величина, обратная целевой функции в i-ой точке. Обычно применяют строго положительную целевую функцию. Другая возможная мера приспособленности использовать ранжирование (классификацию) членов популяции. В этом случае целевая функция может быть вычислена не очень точно при условии, если она обеспечивает правильное ранжирование.

3. Селекция. Алгоритм селекции выбирает из членов популяции (хромосом), какие из них должны принять участие в качестве родителей с целью создания потомства для следующего поколения. Обычно вероятность отбора хромосом для этой цели пропорциональна присущей им степени приспособленности. Основная идея отбора состоит в том, чтобы членам с степенью приспособленности выше средней позволить размножаться и тем самым заменить члены со степенью приспособленности ниже средней. Родители (хромосомы) отбираются, используя метод колеса рулетки, как показано на рис. 4. Каждому родителю может быть сопоставлен сектор колеса рулетки, величина которого устанавливается пропорциональной степени приспособленности данного родителя (данной хромосомы). Поэтому, чем больше степень приспособленности, тем больше сектор на колесе рулетки. Все колесо рулетки соответствует 1, т.е. накопленной сумме вероятностей отбора всех родителей (всех хромосом) рассматриваемой популяции 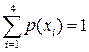. Каждому i -му родителю соответствует сектор колеса, определяемый в данном случае как

,

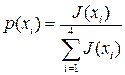где - степень приспособленности i -го родителя, 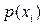- вероятность отбора (селекции) i -го родителя, 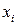- значение i -ой хромосомы. Отбор родителя может быть представлен как результат поворота колеса рулетки, если «выигравший», т.е. выбранный родитель относится к выпавшему сектору этого колеса. Очевидно, чем больше сектор, тем больше вероятность победы соответствующей хромосомы. Поэтому вероятность выбора данного родителя оказывается пропорциональной степени ее приспособленности. Если всю окружность колеса рулетки представить в виде цифрового интервала [0,1], то выбор родителя можно отождествить с выбором числа из интервала [ a, b ], где a и b обозначают соответственно начало и окончание фрагмента окружности, соответствующей этому сектору колеса; очевидно, что 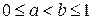. В этом случае выбор с помощью колеса рулетки сводится к выбору числа из интервала [0,1], которое соответствует конкретной точке на окружности колеса.

Так для примера на рис. 4 есть четыре кандидата P1, P2, P3 и P4 на выбор в качестве родителей, имеющих вероятность отбора, полученную с помощью степени приспособленности, 0.5, 0.3, 0.15 и 0.05 соответственно. Для этого примера, если колесо рулетки поворачивается последовательно четыре раза, P1 может быть выбран дважды, P2 и P3 один раз и P4 ни разу.

Рис. 4

4. Скрещивание. Операторы скрещивания генерируют новые хромосомы, которые, надеются, сохранят хорошие свойства от предыдущей генерации. Операция скрещивания обычно применяется к выбранной паре родителей с вероятностью, равной скорости скрещивания. При одноточечном скрещивании точка скрещивания в генетическом коде выбирается случайным образом, и две хромосомы-родители обмениваются своими последовательностями бит, расположенными справа от этой точки. Возьмем для примера две хромосомы, скажем P1 и P2

Если точка скрещивания расположена между пятым и шестым битами, цифры, написанные курсивом обмениваются местами по вертикали. Две новых хромосомы, их потомки П1 и П2 будут выглядеть так

При двухточечном скрещивании выбираются две точки скрещивания и части последовательностей хромосом, расположенные между двумя этими точками, обмениваются местами. В результате такого обмена получают двух детей от этих родителей. Фактически родители переносят фрагменты своих собственных хромосом на хромосомы своих детей. При этом такие дети, надеются, способны превосходить по степени приспособленности своих родителей, если они получили хорошие гены от обоих родителей.

6. Мутация. Оператор мутации может создать самопроизвольно новые хромосомы. Самый распространенный метод случайным образом изменять биты в генах потомков, например с 0 на 1с весьма небольшой вероятностью, определяемой скоростью мутации. Мутация предотвращает сходимость популяции к локальному минимуму. Скорость мутации должна быть невысокой, чтобы не потерять хорошие гены. Мутация обеспечивает защиту от слишком раннего завершения алгоритма (в случае выравнивания всех хромосом и целевой функции).

Процесс репродукции очередных поколений продолжается до тех пор, пока все потомки не будут иметь примерно одну ту же степень приспособленности. В ряде случаев, все потомки, в конце концов, имеют одну и ту же генетическую структуру (одни и те же степени приспособленности), которая представляет глобальный минимум. В других случаях может быть извлечено несколько решений, называемых кластерами. В последнем случае проектировщик системы должен сам принять решение, какое из них считать наилучшим решением.

Заметим, что выше было дано только лишь общее описание основных черт генетического алгоритма. Конкретные его детали весьма отличаются от описанных выше.

Алгоритм. Пример простого генетического алгоритма для задачи максимизации состоит из следующих этапов (рис. 4,а):

1. Инициализировать популяцию с генерируемыми случайным образом особями (решениями) и вычислить значение функции (степень) приспособленности для каждой особи.

2. а) Отобрать из популяции два члена с вероятностью, пропорциональной их степени приспособленности.

б) Осуществить скрещивание с вероятностью, равной скорости скрещивания.

в) Осуществить мутацию с вероятностью, равной скорости мутации.

г) Повторять этапы с а) до г) до тех пор, пока число членов не будет достаточно, чтобы сформировать следующее поколение.

3. Повторять этапы 2 и 3 до тех пор, пока не будут удовлетворяться условия останова алгоритма.

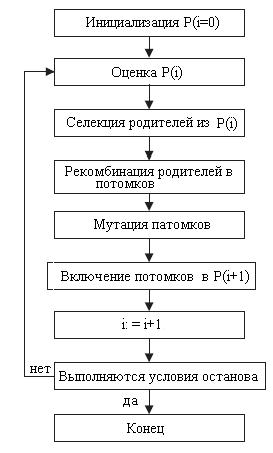
Если скорость мутации высокая (выше 0,1), эффективность алгоритма будет такая же плохая, как в случае использования слепого случайного поиска.

Пример. Пусть система имеет функцию приспособленности

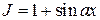, (12)

как показано на рис. 5.

Рис. 5

Предположим, что область решений включает 31 значение и что каждое решение может быть представлено пятиразрядными двоичными числами в диапазоне от 00000 до 11111. Поэтому значение a в уравнении (12) равно 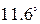(0.203 рад). Если популяция включает четыре гена, то путем подбрасывания монеты (орел=1, решка=0) создаем начальную популяцию

00101 11110 00001 00011

Найдем потомков из начального и последующих поколений.

Из рис. 5 видно, что оптимальное решение имеет место тогда, когда

(индекс 10 указывает на десятичное число), или (индекс 2 указывает на двоичное число).

Таблица 1 показывает, как происходит отбор родителей для спаривания (размножения) из начальной популяции. Родители (хромосомы) отбираются, используя метод рулетки, как показано на рис. 4. Каждому родителю может быть сопоставлен сектор колеса рулетки, величина которого устанавливается пропорциональной степени приспособленности J=f (x_i) данного родителя (данной хромосомы x_i). Поэтому, чем больше степень приспособленности, тем больше сектор на колесе рулетки. Все колесо рулетки соответствует 1, т.е. накопленной сумме вероятностей отбора всех родителей (всех хромосом) рассматриваемой популяции 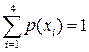. Каждому i -му родителю соответствует сектор колеса, определяемый в данном случае как

,

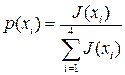где - степень приспособленности i -го родителя, 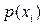- вероятность отбора (селекции) i -го родителя, 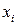- обозначение i -ой хромосомы. Здесь

сумму называют полной приспособленностью рассматриваемой популяции.

Отбор родителя может быть представлен как результат поворота колеса рулетки, если «выигравший», т.е. выбранный родитель относится к выпавшему сектору этого колеса. Очевидно, чем больше сектор, тем больше вероятность победы соответствующего родителя (соответствующей хромосомы). Поэтому вероятность выбора данного родителя оказывается пропорциональной степени его приспособленности. Если всю окружность колеса рулетки представить в виде цифрового интервала [0,1], то выбор родителя можно отождествить с выбором числа из интервала [ a, b ], где a и b обозначают соответственно начало и окончание фрагмента окружности, соответствующей этому сектору колеса; очевидно, что 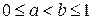. В этом случае выбор с помощью колеса рулетки сводится к выбору числа из интервала [0,1], которое соответствует конкретной точке на окружности колеса.

Так в таблице 1 есть четыре кандидата P1, P2, P3 и P4 на выбор в качестве родителей, имеющих вероятность отбора, полученную с помощью степени приспособленности, 0.342, 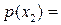0.146, 0.222 и 0.290 соответственно. Эти значения определяют секторы колеса рулетки (рис. 5).

Розыгрыш с помощью колеса рулетки сводится к случайному выбору числа из интервала [0,1], указывающего на соответствующий сектор на колесе, т.е. на конкретного родителя.

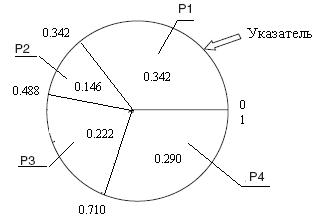
Рис. 5

При этом значение накопленной (совокупной) вероятности в Таблице 1 используется, как изложено ниже:

Значения между 0 и 0.342 приводят к отбору Родителя 1,

Значения между 0.343 и 0.488 приводят к отбору Родителя 2,

Значения между 0.489 и 0.710 приводят к отбору Родителя 3,

Значения между 0.710 и 1.000 приводят к отбору Родителя 4.

Допустим, что разыграны следующие числа:

0.326. 0.412. 0.862 и 0.067.

Это означает выбор родителей

Р1 Р2 Р4 Р1.

Отсюда Родитель 1 был выбран дважды, Родители 2 и 4 один раз и Родитель 3 ни разу. Отобранные родители были спарены случайным образом с помощью случайного выбора точек скрещивания. Степень приспособленности первого поколении потомков приведена в Таблице 2.

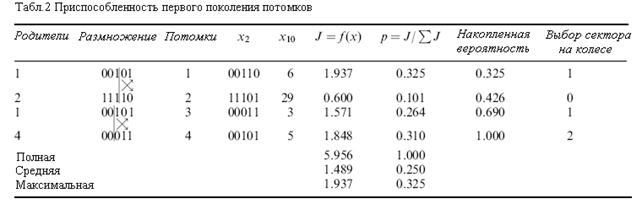
Из Таблиц 1 и 2 следует, что полная приспособленность начальной популяции была 5.412, в то время, как полная приспособленность их потомков составила 5.956, т.е. увеличилась на 10%. Заметим, что если каждый из потомков давал идеальное решение, они бы привели к значению полной приспособленности или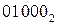, т.е максимальная приспособленность, которую может дать любая популяция определяется как.

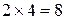Следующий поворот колеса рулетки (генератора случайных чисел) создает значения: 0.814, 0.236, 0.481 и 0.712, определяемые по правилам рулетки и показанные в таблице 2.

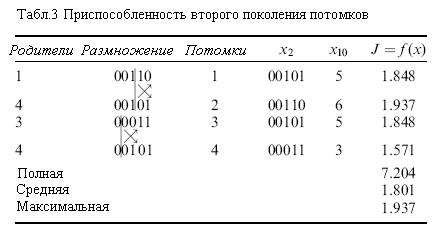
Вторая генерация потомков показана в таблице 3. Из нее видно, что полная приспособленность второго поколения рана 7.204 или на 33% выше, чем у начальной популяции. Т.к. два самых значимых бита у каждого потомка второго поколения равны 00, то последующие размножения путем скрещивания не приведут к появлению двоичных чисел, больших, чем 00111 или 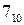. Если все четыре потомка имеют эти значения 00111, то полная приспособленность для популяции составляет 7.953, которая близка, но не равна идеальной полной приспособленности 8.0, как пояснено ранее. Однако, если с помощью мутации изменить в конкретном потомке одну из самых значимых бит с 0 на 1, то можно постепенно достигнуть идеального значения. Следует обратить внимание на небольшое число популяций, использованных в этом примере.

Генетические нечеткие системы (Извлечение нечетких знаний с помощью генетических алгоритмов)

Нечеткие системы успешно применяются в задачах моделирования и управления, и в значительном числе приложений. В большинстве случаев ключом для успешного применения служит способность нечетких систем встраивать знания экспертов. В прошлое десятилетие на успешную предысторию, отсутствие способностей к обучению у нечетких систем, вызвали интерес к изучению нечетких систем, дополненных способностями к обучению.

Двумя самыми успешными подходами оказались попытки их гибридизации, осуществленные в рамках мягких вычислений с помощью других технологий, таких как, нейронные сети и эволюционные вычисления, которые придают нечетким системам способность к обучению (рис. 5). Нейро-нечеткие системы являются одним из самых успешных и очевидных направлений этих усилий. Другой подход гибридизации приводит к генетическим нечетким системам (ГНС).

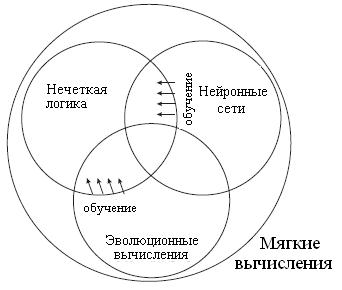
Рис. 5

ГНС в сущности представляет собой нечеткую систему, расширенную за счет процесса обучения, основанного на генетическом алгоритме (ГА). Так как ГА являются поисковыми алгоритмами, которые базируются на естественной генетике, что обеспечивает способность робастного поиска в сложных пространствах, то они предлагают обоснованный подход к решению проблем, требующих эффектных и эффективных поисковых процессов.

Анализ литературы показывает, что самыми заметными приложениями ГНС являются генетические нечеткие лингвистические системы (ГНЛС), в которых генетический процесс обучает или настраивает различные компоненты нечетких лингвистических систем, т.е. систем построенных исключительно с помощью правил в отличие от нечетких систем Такаги-Сугено. Рис. 5 показывает эти концепции для системы, в которой генетическое проектирование и нечеткие рассуждения являются двумя основными составляющими. В этой системе ряд параметров находят путем настройки или обучения, используя ГА.

Недостатки проектирования нечетких лингвистических систем с помощью экспертов:

· Не всегда можно найти сведущего эксперта;

· Извлечение знаний из эксперта отнимает много времени;

· Системы, построенные на приобретенных с помощью эксперта знаниях, работают плохо.

Поэтому приходится применять экспериментально полученные данные для обучения нечеткой системы.

Генетические алгоритмы не были специально разработаны как методы машинного обучения, подобно нейронным системам. Однако не является секретом, что задача обучения может быть сформулирована как оптимизационная задача, и таким образом она может быть решена с помощью эволюционных алгоритмов.

Так как они обладают большой вычислительной мощностью для поиска решений задач в сложных плохо определенных пространствах, то это позволяет успешно применять ГА для большого круга проблем машинного обучения и извлечения данных. Присущая им гибкость и способность встраивать полученные от экспертов знания являются весьма важным свойством с точки зрения решаемых задач.

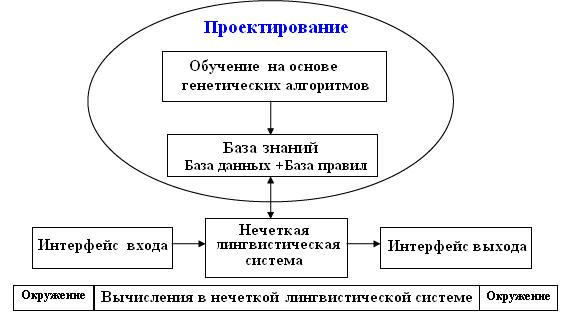
Рис. 6

Другие подходы включают генетические нейронечеткие системы и генетическую нечеткую кластеризацию.

Дата добавления: 2014-01-07