После интегрирования уравнений (2) получим

.

После дифференцирования по X получим

Перейдем к дифференциальным параметрическим уравнениям,

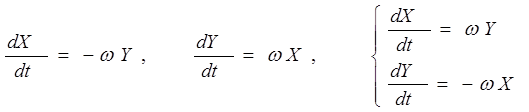(2)

где w - параметр.

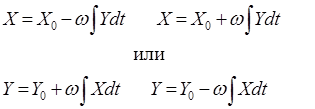(3)

где X0, Y0 - координаты начальной точки окружности.

Система уравнений (3) является решением системы дифференциальных уравнений (2). Аналоговая модель для решения этой же системы имеет следующий вид:

Аналоговая модель для решения этой же системы представлена на рисунке 12.1.

Модель составлена из двух интеграторов, соединенных перекрестными связями, сумматоров, учитывающих начальные условия, и согласователей знаков. Согласование знаков необходимо для задания направления движения. Если в системе уравнений (3) интеграл от Y берется с минусом, а от X с плюсом, то движение происходит против часовой стрелки. Если наоборот интеграл Y, берется со знаком плюс, а интеграл от X со знаком минус, то движение задается по часовой стрелке.

Построим аналогичную структуру для воспроизведения уравнения прямой линии. В режиме линейной интерполяции справедливы уравнения

,

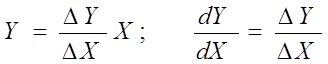где DX, DY - заданные в кадре конечные приращения.

Полученное дифференциальное уравнение может быть приведено к двум параметрическим

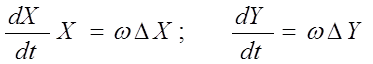
Аналоговая модель для решения этой системы дифференциальных уравнений представляет собой два независимых интегратора

Решением смоделированной системы уравнений и будет уравнение заданной прямой.

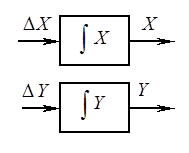
Как видим, задачи интерполяции прямой и окружности решаются с помощью однотипных структур, связи в которых программируются соответственно признаками: “линейная интерполяция“, “круговая интерполяция”.

Базовым элементом структуры является интегратор. Представленные структуры повторены в интерполяторе полностью, однако, с особенностями, присущими цифровым вычислительным блокам вообще и цифровым интерполяторам в частности.

Рассмотрим математическую сторону процесса цифрового интегрирования в интеграторе X при круговой интерполяции. Приближенные оценки S интеграла по формулам прямоугольников и трапеций соответственно равны:

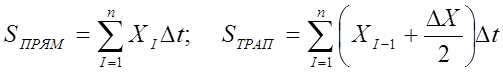
Особенностью интерполятора, построенного по этому принципу, является то, что процесс вычислений непосредственно не связан по времени с процессом выдачи управляющих команд. В этой связи не играют роли масштабные множители в интерполяторах; важно лишь, чтобы выдерживались масштабные соотношения между интеграторами. С учетом сказанного в качестве оценок интеграла можно принять

.

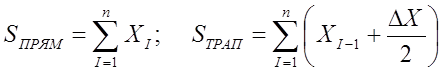Дата добавления: 2014-01-07