Величина угла между прямыми

В этом пункте все уравнения прямых и координаты точек даны в ортонормированном репере 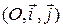на плоскости 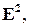а координаты векторов – в соответствующем базисе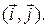

Пусть прямые 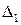и 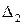на плоскости 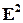заданы общими уравнениями:

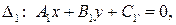
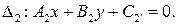
В общем случае прямые 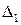и 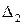пересекаются в одной точке и образуют 4 угла, величины которых – числа 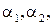такие, что 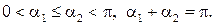Поскольку 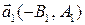и – направляющие векторы прямых, то при любом варианте расположения прямых величину наименьшего из углов можно найти по формуле:

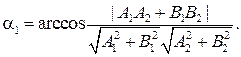
Пусть известны угловые коэффициенты 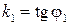и 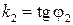прямых 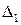и 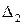соответственно, пересекающихся в одной точке. Можно считать, что 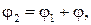где 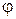– величина угла поворота первой прямой вокруг точки пересечения до совмещения со второй прямой (рис. 10). Тогда 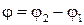и, следовательно, если 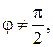то

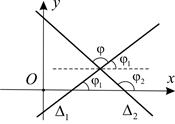
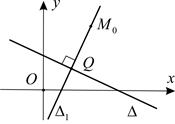
Рис. 10 Рис. 11

Условие перпендикулярности прямых (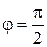) эквивалентно условию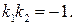

Дата добавления: 2014-01-07