Расстояние от точки до прямой. В этом пункте, как и в предыдущем, все уравнения прямых и координаты точек даны в ортонормированном репере на плоскости

В этом пункте, как и в предыдущем, все уравнения прямых и координаты точек даны в ортонормированном репере 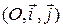на плоскости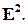

Пусть прямая задана общим уравнением Получим формулу для вычисления расстояния 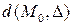от точки 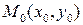до прямой Известно, что где – основание перпендикуляра, опущенного из точки 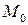на прямую Точка есть точка пересечения прямой и прямой 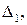проходящей через точку 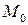и перпендикулярной прямой (рис. 11). Запишем параметрические уравнения прямой 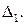проходящей через точку 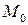и перпендикулярной прямой В качестве направляющего вектора этой прямой можно взять вектор – нормальный (перпендикулярный) вектор прямой Получим:

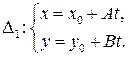
Для нахождения координат точки надо решить систему уравнений:

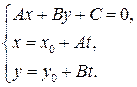
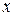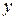Поставим в первое уравнение системы выражения и через 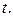Получим уравнение с неизвестной решением которого является число 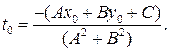Таким образом,

Дата добавления: 2014-01-07