
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Доказательство. Знакоположительные ряды. Достаточные признаки Теорема 14.1.6 (признак сравнения) Пусть даны два ряда с положительными членами и
|
|
|
|
Сходимости.
Знакоположительные ряды. Достаточные признаки
| Теорема 14.1.6 (признак сравнения) |
Пусть даны два ряда с положительными членами 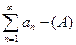 и и 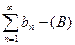 , причем каждый член ряда (А) не превосходит соответствующего члена ряда (B), т.е. при любом n an £ bn (14.1.6) , причем каждый член ряда (А) не превосходит соответствующего члена ряда (B), т.е. при любом n an £ bn (14.1.6)
|
| Тогда: |
| а) если сходится ряд (B), то сходится и ряд (А), причем сумма ряда (А) не превосходит суммы ряда (B); |
| б) если расходится ряд (А), то расходится и ряд (В). |
а) Пусть Sn (А) и Sn (B) – частичные суммы рядов (А) и (В) соответственно, S(B) – сумма ряда (B), т.е. существует предел 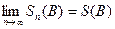 . Очевидно,
. Очевидно,  в силу неравенства (14.6), а
в силу неравенства (14.6), а 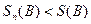 , т.к. все члены ряда (B) положительны (bn>0).
, т.к. все члены ряда (B) положительны (bn>0).
Из обоих неравенств следует 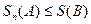 , т.е. последовательность частичных сумм
, т.е. последовательность частичных сумм 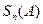 ряда (А) ограничена. Кроме того, последовательность частичных сумм ряда (А) монотонно возрастает, т.к. все аn >0, откуда
ряда (А) ограничена. Кроме того, последовательность частичных сумм ряда (А) монотонно возрастает, т.к. все аn >0, откуда 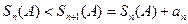
Следовательно, на основании признака существования предела (5.3.6) существует 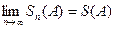 , т.е. ряд (А) сходится.
, т.е. ряд (А) сходится.
Из условия  на основании свойства (т. 5.1.4) пределов получаем
на основании свойства (т. 5.1.4) пределов получаем 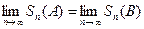 , т.е
, т.е 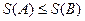 , что и требовалось доказать.
, что и требовалось доказать.
б) пусть ряд (А) расходится, т.е 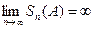 , но из условия (14.1.6)
, но из условия (14.1.6) 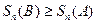 . Переходя к пределу, получаем
. Переходя к пределу, получаем 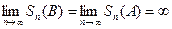 , а это означает, что
, а это означает, что 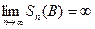 , т.е. ряд (B) расходится.
, т.е. ряд (B) расходится.
Примеры. Исследовать сходимость рядов.
1. 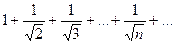
Сравним данный ряд с гармоническим рядом 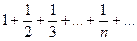 Достаточно сравнить общие члены рядов. Очевидно
Достаточно сравнить общие члены рядов. Очевидно 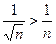 , но гармонический ряд расходится, следовательно, и данный ряд
, но гармонический ряд расходится, следовательно, и данный ряд 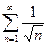 также расходится.
также расходится.
2. 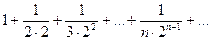
Сравним данный ряд со следующим рядом:
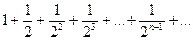 Этот ряд сходится, как геометрическая прогрессия со знаменателем
Этот ряд сходится, как геометрическая прогрессия со знаменателем 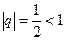 . Т.к.
. Т.к. 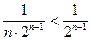 , тогда и данный ряд сходится.
, тогда и данный ряд сходится.
Недостаток признака сравнения заключается в необходимости привлекать другие ряды, что бывает не всегда просто, и относительно которых также следует решать вопросы их сходимости. Кроме того, необходимо доказывать в каждом случае выполнимость неравенства (14.6). Однако достаточно часто удобно использовать эталонные ряды, к которым можно отнести сходящийся геометрический ряд (прогрессия) 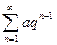 при |q|<1, гармонический ряд
при |q|<1, гармонический ряд 
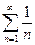 и обобщенный гармонический ряд
и обобщенный гармонический ряд 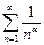 , который сходится, если
, который сходится, если 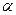 <1 и расходится, если
<1 и расходится, если 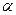 ³1 (было показано выше)
³1 (было показано выше)
Наряду с рассмотренным признаком сравнения рассмотрим еще один.
| Теорема 14.1.7 (предельный признак сравнения). |
Если 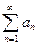 и и 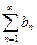 – ряды с положительными членами и существует конечный предел отношения их общих членов – ряды с положительными членами и существует конечный предел отношения их общих членов 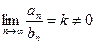 , то оба ряда одновременно сходятся, либо расходятся (ведут себя одинаково) , то оба ряда одновременно сходятся, либо расходятся (ведут себя одинаково)
|
Доказательство. Пусть 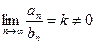 .
.
По определению предела числовой последовательности (тема 5.1) для любого e>0 существует такой номер N, что для всех n >N выполняется неравенство 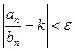 , которое можно записать следующим образом
, которое можно записать следующим образом 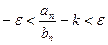 , или
, или 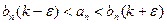
 (14.1.7)
(14.1.7)
Используем признак сравнения и свойства сходящихся рядов применительно к двойному неравенству (14.1.7). Если ряд 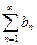 сходится, то сходится и ряд
сходится, то сходится и ряд 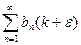 (теорема 14.1.2). Но на основании признака сравнения сходится и ряд
(теорема 14.1.2). Но на основании признака сравнения сходится и ряд 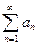 . Предположим, сходится ряд
. Предположим, сходится ряд 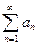 , но тогда сходится и ряд
, но тогда сходится и ряд 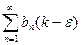 , а значит и сходится и ряд
, а значит и сходится и ряд 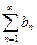 . Предположим ряд
. Предположим ряд 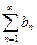 расходится, но тогда расходится и ряд
расходится, но тогда расходится и ряд 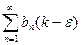 , а следовательно расходится и ряд
, а следовательно расходится и ряд 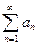 ; если расходится
; если расходится 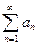 , то аналогично рассуждая, получаем, что расходится и ряд
, то аналогично рассуждая, получаем, что расходится и ряд 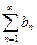 .
.
Пример. Исследовать сходимость ряда 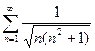 .
.
Сравним с рядом 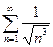 , который сходится (
, который сходится (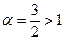 )
)
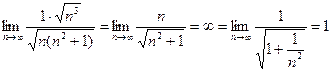
Теорема 14.1.8. Пусть даны два ряда 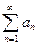 (А) и (А) и 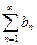 (В). Если хотя бы начиная с некоторого номера выполняется неравенство (В). Если хотя бы начиная с некоторого номера выполняется неравенство 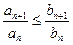 , то если сходится ряд (В), то сходится и ряд (А); если расходится ряд (А), то расходится и ряд (В). , то если сходится ряд (В), то сходится и ряд (А); если расходится ряд (А), то расходится и ряд (В).
|
Доказательство. Пусть 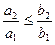 ,
, 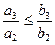 , …
, … 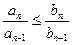 .
.
Тогда 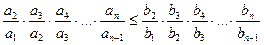 или
или 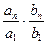 . Если ряд
. Если ряд 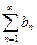 сходится, то сходится и ряд
сходится, то сходится и ряд 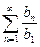 , следовательно на основании признака сравнения (теорема 6) сходится и ряд
, следовательно на основании признака сравнения (теорема 6) сходится и ряд 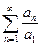 , значит, сходится и ряд (А)
, значит, сходится и ряд (А) 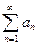 . Если
. Если  расходится ряд (А), то расходится и ряд
расходится ряд (А), то расходится и ряд 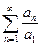 , а значит, и ряд
, а значит, и ряд 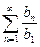 . Но тогда расходится и ряд (В).
. Но тогда расходится и ряд (В).
Выше было отмечено, что признаки сравнения неудобны тем, что требуют привлечения других рядов, желательно хорошо знакомых, которых не так много. Целесообразно рассмотреть признаки, когда ряд как бы говорил сам за себя.
|
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 662; Нарушение авторских прав?; Мы поможем в написании вашей работы!