
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Иерархия математической модели
|
|
|
|
Блочно-иерархический подход к проектированию включает в качестве своей основы иерархию ММ. Деление модели по иерархическим уровням (уровням абстрагирования) происходит по степени детализации абстрагируемых свойств. При этом на каждом иерархическом уровне используются свои понятия «система» и «элементы». Так система n-го уравнения рассматривается как элемент на соседнем более высоком (n-1) уровне абстрагирования.
Иерархия моделей – это взаимосвязь и взаимоподчиненность моделей различных свойств объекта, описанных в виде, например, математических зависимостей, на каждом уровне абстрагирования.
Уровень абстрагирования – описание объекта по сложности взаимодействия функциональных связей.
Представим структуру некоторого объекта в виде множества элементов и связей между ними. Выделим в соответствии с БИП в структуре объекта некоторые подмножества элементов и назовем их блоками (на рис.4.1 показаны штриховыми линиями). Пусть состояние каждой связи характеризуется одной переменной vi, zj или uk.
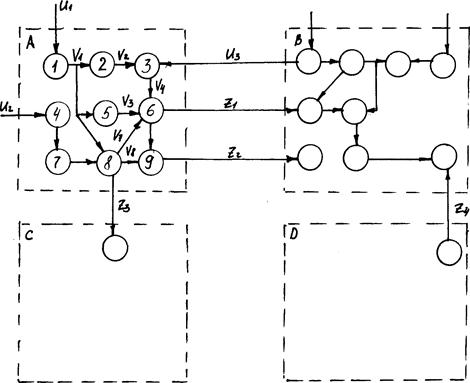
Рис. 4.1. Представление структуры объекта
vi – переменная, относящаяся к внутренним связям между элементами данного блока;
zj – переменная, относящаяся к выходам блока;
uk – переменная, характеризующая входные связи между блоками;
Поясним понятие полной модели и макромодели.
Полная модель блока – это модель, составленная из моделей элементов с учетом меж элементных связей, т. е. модель, описывающая как состояние выходов, так и состояние каждого из элементов блока. Моделями элементов (vi) блока А являются уравнения, связывающее входные (uk) и выходные (zj) переменные:
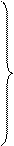 f1(v1, u1) = 0
f1(v1, u1) = 0
f2(v1, v2) = 0
f3(v2, u3, v4) = 0 (4.1)
………………
f9(v8, v9, z2) = 0
Полная модель блока есть система уравнений
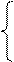 |
F(V, U)=0
Z=Ψ(V, U), (4.2)
где V, U, Z – обобщенные векторы внутренних, входных и выходных переменных блока.
При большом количестве элементов, размерность вектора V и порядок системы уравнений (4.2) становится большим и требует упрощения.
При переходе к более высокому иерархическому уровню упрощения основаны на исключении из модели вектора внутренних переменных V. Полученная модель представляет собой систему уравнений вида:
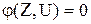 (4.3)
(4.3)
Макромодель уже не описывает процессы внутри блока, а характеризует процессы взаимодействия данного блока с другими в составе системы блоков.
Модели (4.2) и (4.3) относятся друг к другу как полная модель и макромодель на n-ом уровне иерархии. На болем высоком уровне (n-1) блок А рассматривается как элемент и макромодель (4.3) становится моделью элемента А. Следовательно, модели (4.1) и (4.3) относятся друг к другу как модели элементов соседних иерархических уровней. Из модели типа (4.3) может быть составлена полная модель системы на (n-1) уровне.
В зависимости от сложности объекта при его проектировании используют большее или меньшее число уровней абстракции. Объединение уравнений, родственных по характеру используемого математического аппарата, приводит к образованию трех укрупненных уровней иерархически функциональных моделей, которые складываются из микро, макро и метоуровней.
На микроуровне используют математические модели, описывающие физическое состояние элементов объекта проектирования. Для моделирования применяют математический аппарат дифференциальных уравнений.
На метауровне с помощью дальнейшего абстрагирования от характера физических (химических, технологических или других процессов) получают информационное описание процессов, протекаемых в объекте. Здесь применяют аппарат анализа систем.
Требования, предъявляемые к математическим моделям
Основными требованиями, которые предъявляются к математическим моделям, являются следующие:
§ адекватность модели;
§ универсальность модели;
§ экономичность модели.
Модель считается адекватной, если она отражает заданные свойства объекта с приемлемой точностью.
Пусть 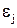 – относительная погрешность модели по j–тому выходному параметру, равная:
– относительная погрешность модели по j–тому выходному параметру, равная:
 = = / /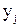 , ,
| (4.4) |
где 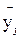 – j-тый выходной параметр, определяемый с помощью модели;
– j-тый выходной параметр, определяемый с помощью модели;
 – текущий параметр, имеющий место в моделируемом объекте.
– текущий параметр, имеющий место в моделируемом объекте.
Тогда погрешность модели  по совокупности учитываемых выходных параметров оценивается вектором
по совокупности учитываемых выходных параметров оценивается вектором
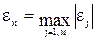 или или 
| (4.5) |
Точность объекта различна в разных условиях функционирования объекта. Эти условия характеризуются внешними параметрами. Если задаться предельной допустимой погрешностью  , то можно выделить область, в которой выполняются условие:
, то можно выделить область, в которой выполняются условие:
|
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 2527; Нарушение авторских прав?; Мы поможем в написании вашей работы!