Методы получения математических моделей

.

Эту область называют областью адекватности модели (ОА).

Пример области адекватности в двумерном пространстве показан на рис. 4.2.

Здесь 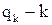-й внешний параметр.

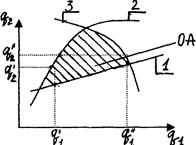
Рис. 4.2. Графическое определение области адекватности функций 4.1, 4.2, 4.3 вида ;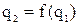

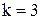
Определение области адекватности для конкретных моделей сложная процедура, требующая больших вычислительных затрат. Эти затраты и трудности быстро растут с увеличением размерности пространства k и числа внешних параметров. Определение области адекватности более трудная задача, чем, например, задача параметрической оптимизации. Поэтому для моделей вновь проектируемых объектов область адекватности не рассчитывают.

Для моделей унифицированных элементов расчет области адекватности оправдывается в связи с однократностью определения области адекватности и многократностью использования моделей при проектировании различных систем. Знание области адекватности позволяет правильно выбирать модели элементов из числа имеющихся и тем самым повышать достоверность машинных результатов.

Универсальность математической модели определяется числом и составом учитываемых в модели входных и выходных параметров.

При определении области адекватности необходимо выбрать совокупность входных и выходных параметров, отражающих учитываемые в модели свойства.

Увеличение числа внешних факторов расширяет применяемость модели, но удорожает работу по определению области адекватности. Выбор совокупности выходных параметров и соответствующий им уровень входных параметров должен быть сравнительно невелик, достаточно стабилен и составляет типовой набор выходных параметров.

Экономичность моделирования характеризуется затратами вычислительных ресурсов, необходимых для реализации модели. Для САПР такими характеристиками являются машинное время и память ЭВМ.

Общие затраты машинного времени и памяти ЭВМ на выполнение в САПР какой-либо проектной процедуры зависят как от особенностей выбранных моделей, так и от методов решения.

Получение математических моделей процессов - процедура неформализованная. Основные решения, касающиеся выбора вида математических соотношений, характера используемых переменных и параметров принимает проектировщик. В то же время такие операции как расчет численных значений параметров моделей, определение области адекватности алгоритмизирования и другие решаются на ЭВМ. Поэтому моделирование объектов обычно проводится специалистами конкретных технических областей с помощью известных традиционных методов теоретических и экспериментальных исследований и технических средств САПР.

Методы получения функциональных моделей делят на теоретические и экспериментальные.

	Выбор свойств объекта, которые подлежат отображению в модели
	Сбор исходной информации о выбранных свойствах объекта
	Анализ, синтез свойств структуры модели

	Построение модели
Теоретическое		Экспериментальные

Получение законов и их математическое описание

Проведение экспериментов по определению закономерностей изменения изучаемых свойств объекта

	Расчет числовых значений и параметров модели
	Оценка точности и адекватности модели

Рис. 4.4. Общая блок-схема последовательности разработки математических моделей

Теоретические методы основаны на изучении физических, механических и электрических закономерностей, протекающих в объекте проектирования, и определения соответствующего этим закономерностям математического описания объекта, обоснование и принятие упрощающих предложений.

Экспериментальные методы основаны на практической реализации и проведении целенаправленных экспериментов по определению закономерностей изменения свойств объекта.

Несмотря на эвристический характер моделирования, имеется ряд общих положений для получения экспериментальных моделей различных объектов: математические методы планирования, алгоритмизация формализуемых операций расчета численных значений параметров; определение области адекватности.

Достаточно общий характер имеют методики реализаций моделей, состоящие из последовательности машинных методов планирования эксперимента; составления алгоритмов расчета численных значений параметров; определения области адекватности.

По форме отражения взаимосвязей в моделируемом объекте модели делятся на следующие виды.

Функциональные модели – это математические модели объектов, отражающие закономерности процессов функционирования объектов. Типичная функциональная модель представляет собой систему уравнений, описывающих свойства проектируемого объекта.

Структурные модели – это математические модели объектов, отражающие структурные свойства объектов, например, их расположение в пространстве, размеры, форма и взаимосвязи между ними.

Геометрические модели – это математические модели объектов, построенные на основе геометрического подобия.

Знаковые модели – это математические модели объектов, представляющие собой упорядоченную запись символов. Знаки взаимодействуют не по физическим законам, а по законам семантики, установленным в той или иной области знаний (программы, схемы, лингвистика).

Мысленные модели – это продукт чувственного восприятия и деятельности абстрактного мышления.

Аналитические модели – это модели, позволяющие получить зависимости выходных параметров от параметров и переменных, характеризующих изучаемое явление. Аналитическое решение математического состояния является обобщеным описанием объекта.

Численные модели – это математические модели объектов, характеризующиеся применением соответствующих численных методов.

Имитационные модели – это модели, реализуемые на ЭВМ в результате использования моделирующих алгоритмов (программ), позволяющих вычислить значение выходных переменных и определить новое состояние системы.

		ММ САПР
Общее				Специальные
		1.Функциональная 2.Структурная 3.Геометрическая 4.Знаковая 5.Мысленная 6.Аналитическая 7.Численная 8.Иммитационная 9.Компьютерная и другие

Рис. 4.5. Формы представления математических моделей

Инвариантная форма – запись соотношений модели с помощью традиционного математического языка без учета метода решения уравнений модели.

Алгоритмическая форма получения моделей – запись соотношений моделей и выбранного численного метода решения в форме алгоритма.

Аналитическая форма – запись модели в виде результата аналитического решения исходных уравнений модели. Обычно модель в аналитической форме представляет собой связь выходных параметров как функции внутренних и внешних параметров, представленную в математической формуле.

Схемная форма (графическая форма) – представление модели, на одном из графических языков (графы, эквивалентные схемы, диаграммы).

Имитационная форма – имитация физических или информационных процессов в объекте при задании различных зависимостей входных воздействий от времени протекания процесса.

Контрольные вопросы для самопроверки

1. Какие модели технологических процессов Вам известны. С какой целью они получены и кто автор этих моделей.

2. Поясните суть иерархии математической модели на известных Вам технологических моделях ткачества.

3. Назовите требования, которым должна соответствовать модель любого процесса.

4. Охарактеризуйте этапы получения теоретической и экспериментальной модели на примере известных Вам моделей процесса ткачества.

5. Назовите известные Вам формы представления моделей. Приведите примеры моделей технологических процессов.

Дата добавления: 2014-01-07