Сталкиваются между собой и со стенками сосуда абсолютно упруго

Законы идеальных газов.

Опр.3.2.1. Идеальным называется газ, молекулы которого

1. имеют пренебрежимо малый собственный объем,

2. не взаимодействуют друг с другом на расстоянии,

Т.е. и деальным газом называется газ, в котором отсутствуют силы межмолекулярного взаимодействия. С достаточной степенью точности газы можно считать идеальными в тех случаях, когда рассматриваются их состояния, далекие от областей фазовых превращений.

Напр., при нормальных условиях (давление 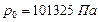и температуре 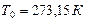) водород, гелий, неон, азот, кислород, воздух и др. можно считать с хорошим приближением идеальными.

Для идеальных газов справедливы законы:

а) Закон Бойля-Мариотта. При изотермическом процессепроизведение объема данной массы газа (масса неизменна) на давление есть величина постоянная . (3.2.1.)

Для двух состояний газа закон записывается в виде, (3.2.1’.)

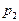где и давление и объем газа в начальном состоянии, и давление и объем газа в конечном состоянии.

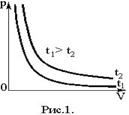
Графически этот закон в координатах РV изображается линией, называемой изотермой (рис.1). Изотермы – гиперболы, расположенные на графике тем выше, чем выше температура процесса.
б) Закон Дальтона. Давление меси различных газов равно сумме парциальных давлений газов, составляющих смесь: . (3.2.2.)

в) Закон Гей-Люссака. При изобарическом процессе

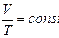. (3.2.3.)

(при постоянном давлении объем данной массы газа прямо пропорционален его абсолютной температуре).

Для двух состояний газа 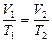, (3.2.3’.)

где и абсолютная температура и объем газа в начальном состоянии, и абсолютная температура и объем газа в конечном состоянии.

Если температура выражена по шкале Цельсия, то , (3.2.3”.)

где температура по шкале Цельсия, объем газа при температуре , объем газа при температуре , коэффициент объемного расширения газов (для идеальных газов , ).

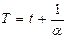Графически зависимость объема от температуры изображается прямой линией – изобарой (рис. 2). При очень низких температурах (близких к –273°С) закон Гей-Люссака не выполняется, поэтому сплошная линия на графике заменена пунктиром.

г) Закон Шарля. При изохорическом процессе . (3.2.4.)

(при постоянном объеме давление данной массы газа прямо пропорционально его абсолютной температуре).

Для двух состояний газа 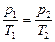, (3.2.4’.)

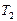где и -абсолютная температура и давление газа в начальном состоянии, и 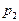- абсолютная температура и давление газа в конечном состоянии.

Если температура выражена по шкале Цельсия, то , (3.2.4”.)

где температура по шкале Цельсия, 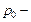давление газа при температуре , 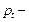давление газа при температуре , коэффициент объемного расширения газов (для идеальных газов , ).

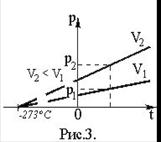
Графическая зависимость давления от температуры изображается прямой линией – изохорой (рис. 3).

д) Закон Авогадро: при одинаковых давлениях и одинаковых температурах и равных объемах различных идеальных газов содержится одинаковое число молекул; или, что то же самое: при одинаковых давлениях и одинаковых температурах грамм-молекулы различных идеальных газов занимают одинаковые объемы.

Например, при нормальных условиях (t = 0°C и p = 1 атм = 760 мм рт. ст.) грамм-молекулы всех идеальных газов занимают объем 22,414 л. Число молекул, находящихся в 1 см ³ идеального газа при нормальных условиях, называется числом Лошмидта; оно равно 2,687*10¹⁹> 1/см³

е) Объединенный газовый закон (уравнение Клапейрона):

- (3.2.5.)

- объединение законов Бойля- Мариотта и Гей – Люссака: для данной массы какого-либо идеального газа произведение давления на объем, деленное на термодинамическую температуру, есть величина постоянная.

Газовая постоянная зависит от химического состава газа и пропорционально его массе. Т.к. ,где удельный объем газа, то уравнение Клапейрона можно переписать: (3.2.5’.)

- у равнение состояния идеального газа.

где р, 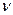и Т - давление, молярный объем и абсолютная температура газа, а 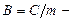удельная газовая постоянная, зависящая только от химического состава газа.

Запишем уравнение (3.2.5.) в форме или 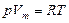, (3.2.6.)

где универсальная (молярная) газовая постоянная, численно равная работе, совершаемой 1 молем идеального газа при изобарном нагревании на один градус: . (3.2.7.)

Ее величина найдена экспериментально.

Для произвольной массы газа объем составит и уравнение состояния имеет вид: , (3.2.8.)

где 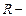универсальная газовая постоянная, 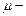масса киломоля газа, масса газа.

Это уравнение называется уравнением Менделеева - Клапейрона.

Следствия уравнения Менделеева – Клапейрона:

1. плотность газа 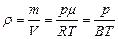. (3.2.9.)
2. число молекул в единице объема 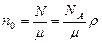. (3.2.10.)
3. концентрация молекул газа . (3.2.11.)

где k - постоянная Больцмана: (3.2.12.)

Уравнение (3.2.6.) можно записать так: 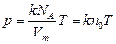(3.2.6’.)

Пример 3.2.1. В баллоне объемом 10 л находится гелий под давлением 10 бар и при температуре 27⁰С. После того, как из баллона было взято 10 г гелия, температура в баллоне понизилась до 17⁰С. Определить давление газа, оставшегося в баллоне.

Решение:

Для начального состояния уравнение Менделеева - Клапейрона имеет вид: . Т.к. объем гелия в конечном состоянии будет таким же (ограничен объемом сосуда), то 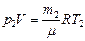. Т.к. 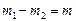, то из данных уравнений найдем массы: и , получим .

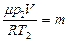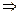
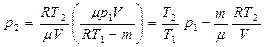
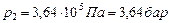
Ответ: .

Пример 3.2.2. Найти массу киломоля смеси 25 г кислорода и 75 г азота.

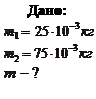
Решение:

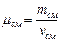, где масса смеси равна сумме компонент смеси: . Число киломолей смеси равно сумме киломолей отдельных газов: 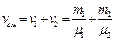, т.к. , , то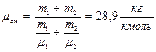

Ответ:

Пример 3.2.3. Определить: 1) сколько молекул содержится в 1 мм³ воды? 2) какова масса молекулы воды? 3) считая условно, что молекулы воды имеют вид шариков, соприкасающихся друг с другом, найти диаметр молекул.

1..Т.к., , томолекул.

2. Масса одной молекулы: .

3. Если молекулы плотно прилегают друг к другу, то можно считать, что на каждую молекулу приходится объем (кубическая ячейка): , где 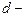диаметр молекулы. Если разделить объем одного киломоля вещества на число молекул в киломоле (число Авогадро), то и .

Пример 3.2.4. Какое количество кислорода выпустили из баллона емкостью 10 л, если при этом показания манометра на баллоне изменились от 14 до 17 ат, а температура понизилась от 27⁰С до 7⁰С?

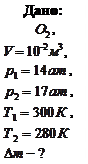
Решение:

Масса выпущенного из баллона газа равна разности между начальной массой кислорода в баллоне и его конечной массой . Т.к. условия в баллоне не слишком отличаются от нормальных, газ можно считать идеальным. Для начального и конечного состояний газа в баллоне получим , .

Внимание: чтобы найти давление газа в баллоне, прибавим к показателям манометра величину атмосферного давления, равную 1 ат. Выразим в единицах СИ числовые значения величин: ,, , , , , 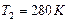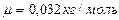. Получаем .

Ответ: .

Пример 3.2.5. Найти молярную массу воздуха, считая, что он состоит по массе из одной части кислорода и трех частей азота.

Решение:

Свойствами идеального газа могут обладать не только химически однородные газы, но и газовые смеси. Чтобы применить уравнение состояния для газовой смеси, ей необходимо приписать некоторую, хотя и лишенную химического смысла, относительную молекулярную массу. Масса смеси в граммах, численно равная ей, представляет собой молярную массу смеси. Величину выбирают такой, чтобы она удовлетворяла уравнению газового состояния, записанному для смеси: 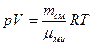. Рассмотрим каждую из газовых компонент: , , где и 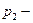парциальные давления каждой компоненты. Для смеси справедлив закон Дальтона: , откуда , а т.к. , то и . Табличные значения , , получаем .

Ответ:

Дата добавления: 2014-01-07