Третий закон

Первый и второй законы термодинамики не позволяют определить значение S₀ энтропии системы при абсолютном нуле температуры (T = 0°К). В связи с этим оказывается невозможным теоретический расчет абсолютных значений энтропии, изохорно-изотермного и изобарно-изотермного потенциалов системы, а также константы равновесия.

На основании обобщения экспериментальных исследований свойств различных веществ при сверхнизких температурах был установлен закон, устранивший указанную трудность и получивший название принципа Нернста или третьего закона термодинамики.

В формулировке Нернста он гласит: в любом изотермическом процессе, проведенном при абсолютном нуле температуры, изменение энтропии системы равно нулю, т. е. , ,

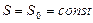независимо от изменения любых других параметров состояния (например, объема, давления, напряженности внешнего силового поля и т. д.). Иными словами, при абсолютном нуле температуры изотермический процесс является также и изоэнтропийным.

Из третьего закона термодинамики следует:

· для всех тел при T = 0°К обращаются в нуль теплоемкости С_p и С_V и термодинамический коэффициент расширяемости .

· вывод о невозможности осуществления такого процесса, в результате которого тело охладилось бы до температуры T = 0°К (принцип недостижимости абсолютного нуля температуры).

Принцип Нернста был развит Планком, предположившим, что S₀ = 0: при абсолютном нуле температуры энтропия системы равна нулю. Физическое истолкование принципа Нернста в формулировке Планка дается в статистической физике.

Условие S₀ = 0 при T = 0°К является следствием квантового характера процессов, происходящих в любой системе при низких температурах, и выполняется только для систем находящихся при Т = 0°К в состоянии устойчивого, а не метастабильного равновесия. На основании гипотезы Планка можно определить абсолютные значения энтропии системы в произвольном равновесном состоянии.

Пример 3.4.4. Один моль идеального двухатомного газа, занимающего объем 12,3 л под давлением 2 атм, нагревается при постоянном объеме до давления 3 атм. Далее газ расширяется при постоянном давлении до объема 24,6 л, после чего охлаждается при постоянном объеме до начального давления и, наконец, сжимается при постоянном давлении до начального объема. Определить: 1) температуру газа для характерных точек цикла; 2) термический к.п.д. цикла.

Решение:

Из уравнения Менделеева – Клапейрона определим температуру газа в состоянии 1: 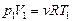, . При изохорическом процессе . При изобарическом процессе . При изохорическом процессе .

Термический (термодинамический) к.п.д. любого цикла определяется формулой 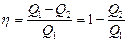, где теплота, полученная газом за один цикл от нагревателя, теплота, отданная газом за один цикл охладителю, теплота, превращаемая в механическую энергию. Термический к.п.д. характеризует степень использования теплоты при превращении ее в механическую энергию, или совершенство цикла, по которому работает тепловая машина.

Теплота, полученная газом при изохорическом процессе (1-2): .

Теплота, полученная газом при изобарическом процессе (2-3): .

Полная теплота, полученная газом от нагревателя: .

Полная теплота, отданная газом охладителю при изохорическом процессе (3-4) и изобарическом процессе (4-5):

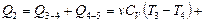
, где .

. Разделим числитель и знаменатель дроби на : , где и .

Пример 3.4.5. В цилиндре под поршнем находится водород массой 0,02 кг при температуре 27⁰С. Водород начал расширяться адиабатически, увеличив свой объем в 5 раз, а затем был сжат изотермически, причем объем газа уменьшился в 5 раз. Найти температуру в конце адиабатического расширения и работу, совершенную газом. Изобразить процесс графически.

Пример 3.4.6. Нагреватель тепловой машины, работающий по обратимому циклу Карно, имеет температуру 200⁰С. Какова температура охладителя, если за счет каждой килокалории тепла, полученной от нагревателя, машина совершает работу 171 ? Потери на трение и теплопередачу не учитываются.

Решение:

Температуру охладителя можно найти, используя выражение для термического к.п.д. машины, работающей по циклу Карно 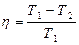, где абсолютная температура нагревателя, холодильника. Отсюда . Термический к.п.д. тепловой машины есть коэффициент использования теплоты. Он выражает отношение теплоты, которая превращается в механическую работу, к теплоте, которая получена рабочим телом тепловой машины из внешней среды (от нагревателя), т.е. 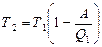. Впишем числовые значения и получим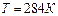

Дата добавления: 2014-01-07