
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Изотермы реальных газов
|
|
|
|
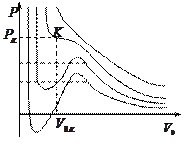
Нанося графически зависимость 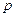 от
от 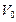 из уравнения Ван-дер-Ваальса для различных
из уравнения Ван-дер-Ваальса для различных 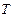 , мы получим ряд изотерм. Каждая из кривых соответствует определенной температуре
, мы получим ряд изотерм. Каждая из кривых соответствует определенной температуре 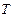 : чем выше температура
: чем выше температура 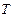 , тем правее и выше лежат на рисунке изотермы. Из рисунка видно, что только при больших температурах
, тем правее и выше лежат на рисунке изотермы. Из рисунка видно, что только при больших температурах 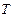 изотерма возрастает с уменьшением
изотерма возрастает с уменьшением 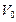 монотонно, напоминая изотерму, соответствующую закону Бойля – Мариотта. На такой изотерме каждому значению давления
монотонно, напоминая изотерму, соответствующую закону Бойля – Мариотта. На такой изотерме каждому значению давления 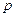 соответствует одно значение молярного объема
соответствует одно значение молярного объема 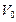 , так же как это имеет место при подчинении газа формуле Менделеева – Клапейрона. При более низких температурах изотермы дают в определенной области давлений и объемов горбы. В этой области, вообще говоря, каждому давлению
, так же как это имеет место при подчинении газа формуле Менделеева – Клапейрона. При более низких температурах изотермы дают в определенной области давлений и объемов горбы. В этой области, вообще говоря, каждому давлению 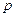 соответствуют три значения объема
соответствуют три значения объема 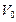 . Область горбов на изотермах относится к переходу вещества из газообразного состояния в жидкое и обратно.
. Область горбов на изотермах относится к переходу вещества из газообразного состояния в жидкое и обратно.
Критическая изотерма
Критическая точка
Для анализа состояний неоднородных систем в термодинамике вводится понятие фазы.
Опр.3.5.1. Фазой называется совокупность всех частей системы, обладающих одинаковым химическим составом, находящихся в одинаковом состоянии и ограниченных поверхностями раздела.
Типы превращения вещества из одной фазы в другую при изменении внешних условий:
· фазовый переход первого рода – выделяется или поглощается теплота (теплота фазового перехода), скачкообразно меняются плотность, удельный и молярный объемы, концентрация компонентов;
· фазовый переход второго рода – теплота не выделяется и не поглощается, плотность изменяется непрерывно, скачкообразно изменяется молярная теплоемкость, коэффициент теплового расширения, удельная электрическая проводимость, вязкость и т.д.
Соотношения между параметрами критического состояния и постоянными Ван-дер-Ваальса:
· Молярный критический объем газа 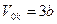 ,
,
· Критическое давление газа 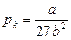 ,
,
· Критическая температура газа 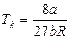 .
.
Коэффициент поверхностного натяжения измеряется силой поверхностного натяжения, действующей на единицу длины любого контура, лежащего на поверхности жидкости: 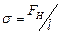 (3.5.2.)
(3.5.2.)
или поверхностной энергией Е, которой обладает каждая единица площади поверхности жидкости: 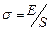 . (3.5.2’.)
. (3.5.2’.)
Прирост поверхностной энергии связан с увеличением поверхности как 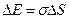 . (3.5.3.)
. (3.5.3.)
Формула Лапласа: избыточное давление, создаваемое в жидкости вследствие кривизны ее поверхности (поверхностное давление), равно
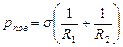 , (3.5.4.)
, (3.5.4.)
где 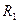 и
и 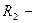 радиусы кривизны двух взаимно перпендикулярных нормальных сечений поверхности жидкости. При этом
радиусы кривизны двух взаимно перпендикулярных нормальных сечений поверхности жидкости. При этом 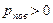 если поверхность выпуклая,
если поверхность выпуклая, 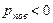 , если вогнутая.
, если вогнутая.
Формула Лапласа в случае сферической поверхности 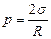 . (3.5.5.)
. (3.5.5.)
Высота поднятия жидкости в капилляре радиуса 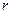 :
: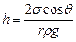 , (3.5.6.)
, (3.5.6.)
где 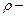 плотность жидкости,
плотность жидкости, 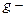 ускорение силы тяжести,
ускорение силы тяжести, 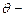 краевой угол.
краевой угол.
Высота поднятия жидкости в капилляре радиуса 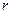 при полном смачивании:
при полном смачивании: 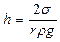 . (3.5.6’.)
. (3.5.6’.)
Высота подъема жидкости между двумя близкими и параллельным друг другу плоскостями 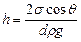 , (3.5.6’’.)
, (3.5.6’’.)
где 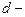 расстояние меду плоскостями.
расстояние меду плоскостями.
Давление насыщающего пара над вогнутой сферической поверхностью жидкости меньше, а над выпуклой - больше, чем над плоской поверхностью, на величину 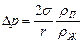 , (3.5.7.)
, (3.5.7.)
где 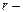 радиус сферы,
радиус сферы, 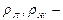 плотности насыщающего пара и жидкости.
плотности насыщающего пара и жидкости.
Пример 3.5.1. В баллоне емкостью 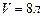 находится 0,3 кг кислорода при температуре 270С. Определить: 1) какую часть объема сосуда составляет собственный объем молекул газа; 2) какую часть давления газа на стенки сосуда составляет внутреннее давление, обусловленное силами притяжения молекул.
находится 0,3 кг кислорода при температуре 270С. Определить: 1) какую часть объема сосуда составляет собственный объем молекул газа; 2) какую часть давления газа на стенки сосуда составляет внутреннее давление, обусловленное силами притяжения молекул.
Решение:
1)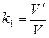 , где
, где 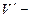 собственный объем молекул. Из уравнения Ван-дер-Ваальса
собственный объем молекул. Из уравнения Ван-дер-Ваальса 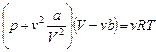 поправка, равная
поправка, равная 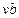 , означает учетверенный собственный объем молекулы, т.е.
, означает учетверенный собственный объем молекулы, т.е. 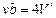
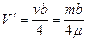 и
и 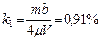 .
. 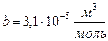 .
.
2)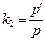 , где
, где 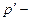 внутреннее давление, обусловленное силами притяжения молекул,
внутреннее давление, обусловленное силами притяжения молекул, 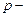 давление, производимое газом на стенки сосуда. Из уравнения Ван-дер-Ваальса
давление, производимое газом на стенки сосуда. Из уравнения Ван-дер-Ваальса 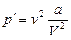
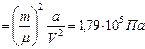 ,
, 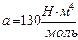 .
. 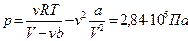 .
. 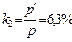 .
.
Пример 3.5.2. Найти добавочное давление внутри мыльного пузыря диаметром 10 см. Какую работу нужно совершить, чтобы выдуть этот пузырь?
Пример 3.5.3. Определить изменение свободной энергии поверхности мыльного пузыря при изотермическом увеличении его объема от 10 см3 до 20 см3.
Пример 3.5.4. В очень прочном закрытом стальном баллоне заключена вода, занимающая при комнатной температуре половину объема баллона. Найти давление (в технических атмосферах) и плотность водяных паров при повышении температуры до 4000С.
Решение:
Из таблицы критических температур возьмем для воды 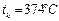 . Т.е. при нагревании воды в баллоне до 4000С она оказалась при температуре выше критической. Следовательно, она вся будет находиться в газообразном (парообразном) состоянии.
. Т.е. при нагревании воды в баллоне до 4000С она оказалась при температуре выше критической. Следовательно, она вся будет находиться в газообразном (парообразном) состоянии.
Плотность водяного пара определим, учитывая, что объем одной и той же массы воды в результате ее нагревания увеличился в 2 раза (массу паров, находящихся под водой при комнатной температуре, можно не учитывать). Т.о. 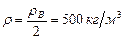 . Т.к. плотность пара в баллоне оказалась громадной по сравнению с плотностями газов при нормальных условиях, то водяной пар можно рассматривать как реальный газ. По уравнению Ван-дер-Ваальса получим:
. Т.к. плотность пара в баллоне оказалась громадной по сравнению с плотностями газов при нормальных условиях, то водяной пар можно рассматривать как реальный газ. По уравнению Ван-дер-Ваальса получим: 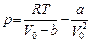 . Здесь
. Здесь 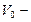 молярный объем, но не объем всей массы пара.
молярный объем, но не объем всей массы пара. 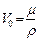 , где
, где 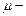 молярная масса пара. Получаем
молярная масса пара. Получаем 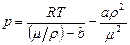 . Табличные значения
. Табличные значения 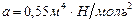 ,
, 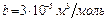 ,
, 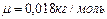 . Получаем
. Получаем 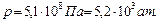
Ответ: 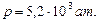
Пример 3.5.5. Определить давление 280 г азота, находящегося при температуре 270С в сосуде, объем которого равен: 1)1 м3; 2) 0,5 л.
Решение:
Чтобы решить вопрос о том, каким следует считать данный газ – идеальным или реальным, - найдем молярный объем газа 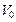 . Пусть в сосуде содержится
. Пусть в сосуде содержится 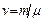 молей газа. Тогда
молей газа. Тогда 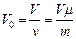 . Т.к. для азота
. Т.к. для азота 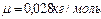 , то 1)
, то 1)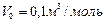 ; 2)
; 2) 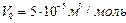 . Сравнивая полученные значения с молярным объемом газа при нормальных условиях
. Сравнивая полученные значения с молярным объемом газа при нормальных условиях 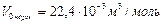 , видим, что в первом случае
, видим, что в первом случае 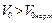 , газ можно считать идеальным. Уравнение идеального газа для одного моля:
, газ можно считать идеальным. Уравнение идеального газа для одного моля: 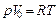 , откуда
, откуда 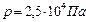 .
.
во втором случае 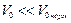 , газ следует считать реальным. Уравнение Ван – дер - Ваальса:
, газ следует считать реальным. Уравнение Ван – дер - Ваальса: 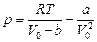 . По таблице
. По таблице 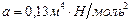 ,
, 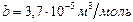 откуда
откуда 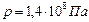 ..
..
Ответ: 1) 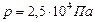 ; 2)
; 2) 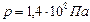 .
.
Пример 3.5.6. Определить массу кислорода в баллоне объемом 10л при температуре 270С и давлениях: 1)1ат; 2) 410 ат.
Пример 3.5.7. Какую работу против сил поверхностного натяжения надо совершить, чтобы выдуть мыльный пузырь радиусом 0,05 м? Чему равно избыточное давление внутри пузыря?
Решение:
Мыльный пузырь представляет собой очень тонкую пленку мыльной воды приблизительно сферической формы. Эта пленка имеет две поверхности – наружную и внутреннюю. Пренебрегая толщиной пленки и считая радиусы обеих сфер одинаковыми, найдем их общую площадь: 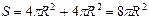 . Т.к. до образования пузыря поверхность мыльной воды, из которой он выдут, была очень мала, можно считать, что мы получили прирост площади
. Т.к. до образования пузыря поверхность мыльной воды, из которой он выдут, была очень мала, можно считать, что мы получили прирост площади 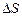 поверхности мыльной воды. Но прирост поверхностной энергии связан с увеличением поверхности как
поверхности мыльной воды. Но прирост поверхностной энергии связан с увеличением поверхности как 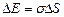 . Совершаемая при выдувании пузыря работа против сил поверхностного натяжения идет на увеличение поверхностной энергии:
. Совершаемая при выдувании пузыря работа против сил поверхностного натяжения идет на увеличение поверхностной энергии:  .
.
Для определения избыточного давления внутри пузыря учтем, что каждая из сферических поверхностей пузыря - наружная и внутренняя – производит вследствие своей кривизны давление на воздух внутри пузыря. Это давление, производимое сферой, найдем по формуле Лапласа, считая 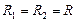 :
: 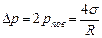 . По таблице
. По таблице 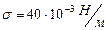 , получим
, получим 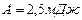 ,
, 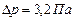 .
.
Ответ: 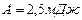 ,
, 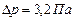 .
.
 Пример 3.5.8. На полированную стеклянную пластинку капнули 0,01 г воды и наложили сверху вторую такую же пластинку. Вода растеклась между пластинками по площади круга радиуса 3 см, не дойдя до ее краев. С какой силой надо растягивать обе пластинки, чтобы их разъединить? Считать, что вода полностью смачивает стекло.
Пример 3.5.8. На полированную стеклянную пластинку капнули 0,01 г воды и наложили сверху вторую такую же пластинку. Вода растеклась между пластинками по площади круга радиуса 3 см, не дойдя до ее краев. С какой силой надо растягивать обе пластинки, чтобы их разъединить? Считать, что вода полностью смачивает стекло.
Решение:
При наложении пластинок свободная поверхность воды вследствие полного смачивания образует вогнутый мениск (см. рис) в виде двух полуокружностей. Следовательно, давление в жидкости, заключенной между пластинами, меньше атмосферного на величину 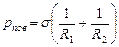 . Под избытком внешнего давления пластины сближаются, вода растекается между ними все более тонким слоем. Этот процесс прекратится, когда жидкость дойдет до краев пластин, после чего мениск распрямится, а поверхностное давление и сила притяжения между пластинами исчезнут, или когда дальнейшее сближение пластин станет невозможным из-за того, что они начнут соприкасаться друг с другом в некоторых точках вследствие неровностей их поверхностей. Именно последний случай имеет место в задаче. Сила притяжения между пластинками
. Под избытком внешнего давления пластины сближаются, вода растекается между ними все более тонким слоем. Этот процесс прекратится, когда жидкость дойдет до краев пластин, после чего мениск распрямится, а поверхностное давление и сила притяжения между пластинами исчезнут, или когда дальнейшее сближение пластин станет невозможным из-за того, что они начнут соприкасаться друг с другом в некоторых точках вследствие неровностей их поверхностей. Именно последний случай имеет место в задаче. Сила притяжения между пластинками 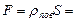
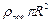 , где
, где 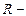 радиус круга растекания жидкости.
радиус круга растекания жидкости.
Радиус кривизны 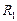 равен половине расстояния между пластинками (по рис.), радиус кривизны
равен половине расстояния между пластинками (по рис.), радиус кривизны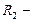 радиус круга растекания жидкости, данный в условии (радиусы рассматриваются во взаимно перпендикулярных плоскостях). Т.к.
радиус круга растекания жидкости, данный в условии (радиусы рассматриваются во взаимно перпендикулярных плоскостях). Т.к. 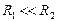 , то
, то 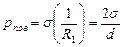 , где
, где 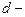 расстояние между пластинками.
расстояние между пластинками. 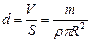 . Получаем
. Получаем 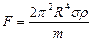 . Чтобы разъединить пластины, их надо растягивать с силой, по крайней мере равной силе их взаимного притяжения. Табличные значения
. Чтобы разъединить пластины, их надо растягивать с силой, по крайней мере равной силе их взаимного притяжения. Табличные значения 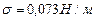 ,
, 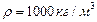 . Получаем
. Получаем 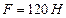 .
.
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 1836; Нарушение авторских прав?; Мы поможем в написании вашей работы!