Неперервні функції та їх властивості

Лекція № 6.

Ответ:.

Означення 6.1. Нехай 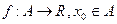і є граничною точкою множини A. Тоді кажуть, що функція є неперервною в точці 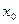, якщо

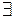
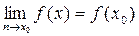(6.1).

Якщо функція неперервна в усіх точках множини , то кажуть, що функція неперервна на множині .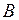

Позначимо через 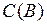клас всіх неперервних функцій на множині 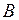, тобто:

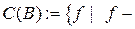неперервна на . Тоді твердження "функція f – неперервна на 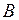" скорочено можна записати як " " і, відповідно, " - неперервна в точці ” - як "".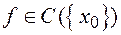

Теорема 6.1 (Про збереження неперервності функцій при арифметичних операціях над ними). 1)Нехай 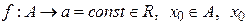- гранична точка множини, тоді функція неперервна в точці

2) Нехай 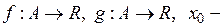гранична множина множиниі 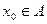. Тоді функції 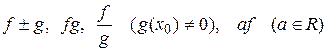теж є неперервними в точці .

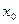Доведення. Досить застосувати означення неперервності функції в точці та теорему про перехід до границі при арифметичних операціях над функціями (теорема 5.4).

Завдання для самостійної роботи 6.1: Навести детальне доведення теореми 6.1.

Теорема 6.2 (Про границю складної функції). Нехай

1) , , - гранична точка множини і

2) де 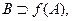точка а є граничною для множини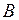, і функція неперервна в точці а. Тоді 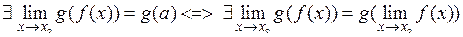(6.2).

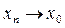Доведення. Скористаємося означення границі функції за Гейне. Нехай послідовність і при . Тоді з умови 1) випливає що при , а з умови 2) маємо, що при 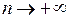. Отже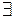 що і потрібно було довести.

Зауваження 6.1. Так як 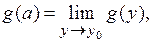то (6.2) можна переписати у вигляді: 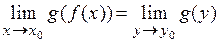(6,3).

Формулу (6.3) ще називають формулою заміни змінної в границі функції, або кажуть, що виконано підстановку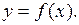

Зауваження 6.2. Нехай функція має скінчену границю у нескінченій точці 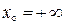або , тобто, . Тоді, якщо доозначити функцію у ціх точках як 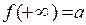або, відповідно, 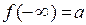, то функція стає неперервною у нескінченій точці.Отже, і теорема 6.2 буде виконуватись і у випадку нескінченої граничної точки .

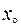Теорема 6.3 (Про неперервність складної функції). Нехай

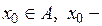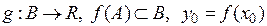, гранична точка множини - неперервна в точці , а також задана функція , і 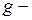неперервна в точці 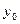. Тоді складна функція 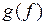неперервна в точці .

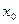Доведення. Дане твердження слідує з означення неперервності функції в точці та з попередньої теореми, в якій потрібно покласти .

Завдання для самостійної роботи 6.2: Навести детальне доведення теореми 6.3.

При обчисленні границь методом заміни змінної часто доводиться використовувати формулу (6.3) в зворотному напрямку, тобто постає питання: чи існує границя функції , якщо відомо, що існує границя складної функції 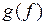. Відповідь на це питання міститься в наступному твердженні:

Теорема 6.4 (Про заміну змінної в границі функції). Нехай:

1), 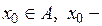гранична точка множини , ;

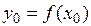2) ;

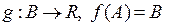3) відображення 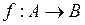є бієкцією, тобто існує обернена функція , і ця функція є неперервною в точці, тобто,;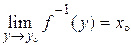

4) композиція функцій - неперервна в точці , і .

Тоді з існування границі в лівій частині рівності (6.3) випливає і її існування в \правій, тобто,

Доведення. Твердження теж випливає з теореми 6.2, якщо її застосувати до функцій 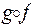та 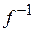. Дійсно, функція 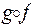- неперервна і має границю 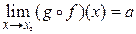, і існує границя , тому . Але отже,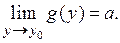Теорема доведена.

Дата добавления: 2014-01-07