
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Неперервність оберненої функції
|
|
|
|
В т еоремі 6.4 фігурує умова існування оберненої функції, тому нас цікавить достатня умова існування оберненої функціїта умови її неперервності.
Теорема 6.10 (Про достатні умови існування оберненої функції). Нехай функція  відображає множину
відображає множину 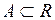 на множину
на множину 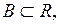 і є строго монотонною функцією. Тоді функція
і є строго монотонною функцією. Тоді функція  має обернену, яка теж є стого монотонною.
має обернену, яка теж є стого монотонною.
Доведення. Поставимо у відповідність кожному елементу  його прообраз
його прообраз 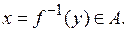 Нам потрібно довести, що для кожного
Нам потрібно довести, що для кожного  існує тільки один прообраз цього елементу і що більшому образу
існує тільки один прообраз цього елементу і що більшому образу  відповідає більший прообраз
відповідає більший прообраз 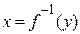 , якщо функція
, якщо функція  - зростаюча, і навпаки - в противному разі.
- зростаюча, і навпаки - в противному разі.
По-перше, існування хоч одного прообразу  випливає з того, що відображення
випливає з того, що відображення  є сюр'єцією, тобто відображенням множини A на множину B.
є сюр'єцією, тобто відображенням множини A на множину B.
По друге, єдиність існування прообразу є наслідком строгої монотонності функції  . Це легко бачити від супротивного. Дійсно, нехай, наприклад, функція
. Це легко бачити від супротивного. Дійсно, нехай, наприклад, функція  є строго зростаючою, і припустимо, що якась точка
є строго зростаючою, і припустимо, що якась точка 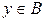 має два прообрази
має два прообрази 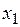 і
і  , які не співпадають,наприклад,
, які не співпадають,наприклад, 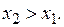 Але тоді, внаслідок строгого зростання функції
Але тоді, внаслідок строгого зростання функції  , виконена нерівність
, виконена нерівність 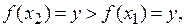 що неможливо. Отже, припущення не вірне, тобто,
що неможливо. Отже, припущення не вірне, тобто, 
По-третє, якщо, наприклад, функція  є строго зростаючою,
є строго зростаючою, 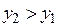 і
і 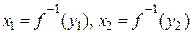 , то тоді
, то тоді 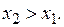 Бо в противному разі нерівність
Бо в противному разі нерівність 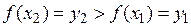 не виконується. Отже, обернена функція
не виконується. Отже, обернена функція 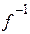 теж є строго зростаючою. Теорему доведено.
теж є строго зростаючою. Теорему доведено.
Теорема 6.11 (Про достатні умови неперевності оберненої функції на відрізку). Нехай 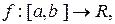 де
де 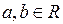 , і нехай:
, і нехай:
1) 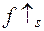 на
на 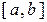 (тобто,
(тобто,  - строго зростає на
- строго зростає на 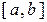 );
);
2) 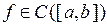 (функція неперервна на
(функція неперервна на 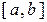 ).
).
Тоді  має обернену функцію
має обернену функцію 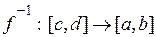 , яка теж строго зростає і є неперервною на
, яка теж строго зростає і є неперервною на 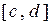 . При цьому,
. При цьому,  .
.
Доведення. За теоремою Больцано-Коші слідує, що відображення  є сюрьєкцією відрізка
є сюрьєкцією відрізка 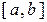 на відрізок
на відрізок  , де
, де  і
і 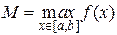 . А за попередньою теоремою випливає, що строго зростаюча функція
. А за попередньою теоремою випливає, що строго зростаюча функція  має обернену функцію
має обернену функцію  , яка теж є строго зростаючою, і, тому,
, яка теж є строго зростаючою, і, тому, 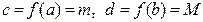 .
.
Доведемо неперервність оберненої функції. Нехай 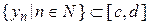 - довільна послідовність точок відрізка
- довільна послідовність точок відрізка 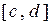 , яка збігається до деякої точки
, яка збігається до деякої точки  цього відрізка. Покажемо, що тоді відповідна послідовність прообразів відображення
цього відрізка. Покажемо, що тоді відповідна послідовність прообразів відображення  збігається до точки
збігається до точки  , тобто,
, тобто, 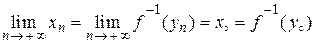 .
.
Від супротивного. Припустимо, що 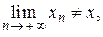 . Тоді існує таке число
. Тоді існує таке число 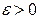 , для якого знайдеться нескінчена підпослідовність
, для якого знайдеться нескінчена підпослідовність  така, що відстань її точок до точки
така, що відстань її точок до точки  не менша за число
не менша за число 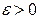 , тобто, має місце нерівність
, тобто, має місце нерівність  . Так як підпослідовність
. Так як підпослідовність 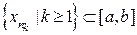 - обмежена, то з неї можна вилучити збіжну до деякої точки
- обмежена, то з неї можна вилучити збіжну до деякої точки 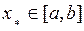 підпослідовність
підпослідовність  , для елементів якої теж виконана нерівність
, для елементів якої теж виконана нерівність 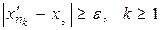 .Таким чином, точка
.Таким чином, точка 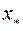 не співпадає з точкою
не співпадає з точкою  ,отже, (за однозначністю функції
,отже, (за однозначністю функції  )
) 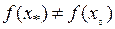 , і при цьому
, і при цьому 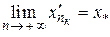 . Тому, за неперервністю функції
. Тому, за неперервністю функції  маємо:
маємо: 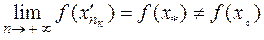 (6.7).
(6.7).
Але послідовність  є підпослідовністю послідовності
є підпослідовністю послідовності  , яка збігається до числа
, яка збігається до числа  . Отже,
. Отже,  , що рівносильно рівності
, що рівносильно рівності  , яка суперечить (6.7). Таким чином, припущення не вірне. Теорему доведено.
, яка суперечить (6.7). Таким чином, припущення не вірне. Теорему доведено.
Теорема 6.12 (Про достатні умови неперевності оберненої функції на інтервалі). Нехай 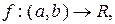 де
де 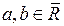 , і нехай:
, і нехай:
1) 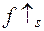 на функції
на функції  ; 2)
; 2) 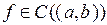 .
.
Тоді  має обернену функцію
має обернену функцію  , яка теж строго зростає і є неперервною на
, яка теж строго зростає і є неперервною на 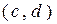 . При цьому,
. При цьому, 
Доведення. Існування і строге зростання оберненої функції 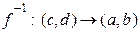 слідує за теоремою 6.10. Доведемо її неперервність. Нехай
слідує за теоремою 6.10. Доведемо її неперервність. Нехай  - довільна точка інтервалу
- довільна точка інтервалу 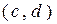 , яка є образом деякої точки
, яка є образом деякої точки 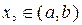 при відображенні
при відображенні  . Тоді знайдеться відрізок, який містить точку
. Тоді знайдеться відрізок, який містить точку  і сам міститься у інтервалі
і сам міститься у інтервалі 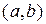 . Наприклад, це відрізок
. Наприклад, це відрізок 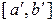 , де
, де
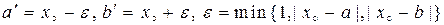 .
.
Тоді на відрізку 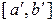 виконуються умови попередньої теореми, і, отже, в точці
виконуються умови попередньої теореми, і, отже, в точці  обернена функція є неперервною, що і потрібно було довести.
обернена функція є неперервною, що і потрібно було довести.
Завдання для самостійної роботи 6.5: Довести, що теореми 6.10 і 6.11 справджуються і за умови строгого спадання функції  .
.
Зауваження 6.4. За теоремами 6.10 і 6.11 слідує, що їх твердження справджуються і за умови задання функції  на пів відрізку
на пів відрізку 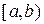 або
або  .
.
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 2258; Нарушение авторских прав?; Мы поможем в написании вашей работы!