Похідна функції та її застосування

Лекція № 8.

Нехай задано функцію . Позначимо: .

Означення 8.1. Якщо існує скінчена границя

,

то ця границя називається похідною функції в точці 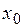і позначується:

або або або .

Таким чином, 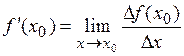(8.1).

Операція знаходження похідної називається диференціюванням функції .

Означення 8.2. Лівою і правою похідною функції в точці 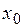називаються відповідно границі:

,

Зауваження 8.1. Похідна функції існує в точці 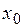тоді і тільки тоді, коли у цій точці існують права та ліва похідні функції , і вони співпадають між собою. Тобто,

(8.2).

Означення 8.3. Будемо говорити, що фyнкція має похідну на множині В, якщо в кожній точці існує похідна . Клас функцій, що мають похідну на множині В, будемо позначати як Тоді,

(8.3).

Теорема 8.1 (Про характеризацію функції, що має похідну). Нехай функція має похідну в точці 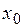. Тоді в деякому околі її можна подати у вигляді

(8.4),

де-нескінченно мала неперервна величина в точці .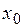

Доведення.

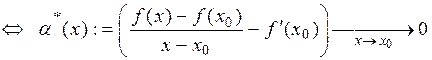
Звідки випливає, що в деякому виколотому околі виконується рівність

(8.4),

де - нескінчено мала величина в точці .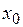

Покладемо, 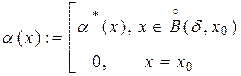. Тоді функція 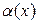буде неперервною нескінченно малою величиною, і при цьому має місце рівність

Що і потрібно було довести.

Теорема 8.2. (Про необхідну умову існування похідної). Нехай функція має похідну в точці , тоді функція в цій точці є неперервною. Тобто,

(8.5).

Доведення. Нехай тоді з попередньої теореми випливає, що існує границя

,

що і потрібно було довести.

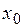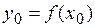Теорема 8.3. (Про похідну складної функції). Нехай функція визначення в деякому околі точки , має в цій точці похідну та приймає значення .Нехай функція визначена в деякому околі точки і теж має похідну Тоді існує похідна складної функції в точці 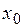, і при цьому

(8.6).

Тобто,

Доведення. Нехай , тоді в деякому околі точки функцію можна подати у вигляді , де -неперервна нескінченно мала величина в точці . Але за неперервностю функції в точці 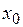випливає, що знайдеться такий - окіл , що для всіх точок маємо 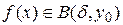. Тоді, підставивши в попередню рівність, отримаємо:

А тому, за існуванням похідних і випливає, що існує границя

При цьому враховано, що за неперервністю функцій в точціі в точці 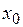випливає неперервність функції , і тому 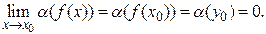Теорему доведено.

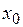Теорема 8.4. (Про арифметичні операції над похідними). Нехай існують похідні і функцій та в точці . Тоді існують і похідні функцій 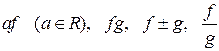(якщо ), і при цьому:

1) , де =.

2) .

3) .

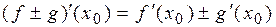4) .

5) .

Доведення. Доведемо, наприклад, третє твердження теореми. Використовуючи теорему 5.4 про збереження арифметичних операцій при взятті границі, отримаємо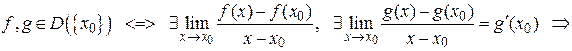

=

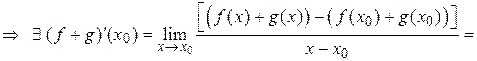
Змінивши в попередніх викладках суму функцій та на їх різницю, одержимо

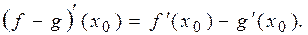
Аналогічно доводяться і інші пункти теореми. Так для п’ятого твердження теореми за теоремами 5.4 і 8.2 маємо: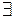

=
.

Де враховано, що з того, що існує похідна , випливає неперервність функції в точці 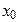. Тому, П’яте твердження теореми доведено.

Завдання для самостійної роботи 8.1: Довести пункти 1),2),4) попередньої теореми.

Теорема 8.5 (Про похідну оберненої функції). Нехай 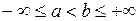і функція задовольняє умовам: .

Тоді існує похідна оберненої функції у відповідній точці , і при цьому 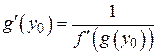, тобто, (8.7).

Доведення. Нехай, наприклад, функція строго спадає на інтервалі, тобто, на . Тоді за теоремою 6.12 про існування і неперервність оберненої функції випливає, що існує обернена неперервна строго спадна функція де і на . Так як і взаємно обернені функції, тоНехай тобто, Тоді, за теоремою 8.1 слідує:

,

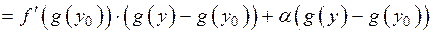де - нескінченно мала неперервна величина в точці 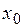, тому - нескінченно мала неперервна величина в точці 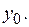Отже,

.

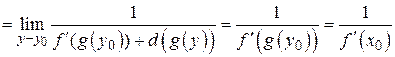Тобто, існує похідна Що і потрібно було довести.

Теорема 8.6 (Про таблицю похідних основних елементарних функцій).

1) .

2) .

3) .

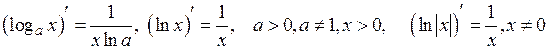4) .

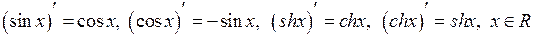5) ,

,

де функція 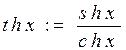називається тангенсом гіперболічним,

а функція - котангенсом гіперболічним.

6)

.

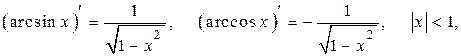
7) на відповідних областях визначення лівих і правих частин рівностей.

Доведення. 1) Нехай , > 0, . Тоді на підставі означення похідної та т еореми 5.10 маємо:

Аналогічно обчислюється похідна степеневої функції у тих випадках, коли вона має ширшу область визначення.

2) Нехай 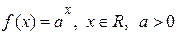. З таких самих міркувань, як і в попередньому пункті доведення, отримаємо:

.

3) Нехай Тоді,

Якщо , то . Тому, .

За теоремою про складне диференціювання маємо: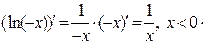

Тому, .

4) Нехай 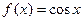, . Тоді,

Так як функція неперервна на R, то , коли . Користуючись формулою зведення кутів тригонометричних функцій та правилом обчислення похідної складної функції, маємо:

Обчислимо похідні гіперболічних функцій: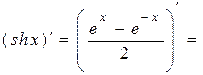

Аналогічно, .

5) Щоб отримати похідну застосуємо теорему про похідну частки:

.

Аналогічно, .

Легко перевірити, що . Дійсно,

.

Тому, .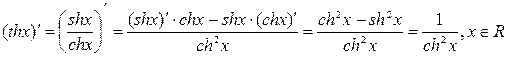

Аналогічно можна отримати: .

6) Знайдемо похідні обернених тригонометричних функцій.

Нехай . Тоді є оберненою функцією, отже, згідно теореми про похідну оберненої функції, маємо

Аналогічно знаходиться похідна інших обернених тригонометричних функцій.

7) Розглянемо функцію . Покажемо, що оберненою до неї є функція . Дійсно,

Тоді, з теореми про похідну оберненої функції випливає, що для довільного дійсного числа існує похідна

Що і потрібно було довести.

Завдання для самостійної роботи 8.2: Довести нерозглянуті формули теореми.

Дата добавления: 2014-01-07