Лекция 10. Закон электромагнитной индукции и уравнение для вихревого электрического поля

Закон электромагнитной индукции и уравнение для вихревого электрического поля. Взаимная энергия контуров с током, энергия магнитного поля. Ток смещения. Дифференциальные и интегральные формы уравнений Максвелла. Закон сохранения заряда.

В 1831 году Фарадей сделал одно из самых фундаментальных открытий в электродинамике: он открыл явлений электромагнитной индукции. Суть явления состоит в следующем. Возьмем катушку, концы которой соединим с гальванометром. При приближении к катушке магнита в цепи возникает индукционный ток и стрелка гальванометра отклоняется. При удалении магнита стрелка отклоняется в противоположную сторону. Аналогично, направление тока меняется, если магнит повернуть на 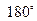. Если двигать катушку, оставляя магнит неподвижным, то стрелка гальванометра также отклоняется. Все это означает, что в контуре с гальванометром появляется ЭДС.

Понять происхождение ЭДС позволяет следующий простой (и схематичный) эксперимент. Рассмотрим конфигурацию проводников изображенных на рисунке 1(пунктирными стрелками показано положительное направление обхода контура):

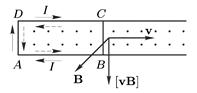
Рис.1.

При движении подвижного проводника 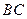так, как показано на рисунке направление тока и силы на положительные заряды будет вниз. Вычислим циркуляцию этой силы по замкнутому контуру (это и будет ЭДС):

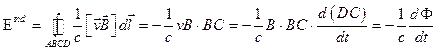(1)

где - магнитный поток через контур. То есть роль сторонней силы играет сила Лоренца. Формула (1) имеет место для произвольного контура и произвольного движения контура. А что будет, если контур неподвижен, а движется магнит, то есть изменяется магнитное поле? Тогда можно перейти в систему отсчета связанную с магнитом, в которой контур будет двигатьсяи в нем возникнет индукционный ток. Само явление индукционного тока от инерциальной системы не зависит. Следовательно, индукционный ток возникнет и в исходной системе, в которой контур неподвижен. К этому же выводу можно прийти из формулы преобразования полей. В системе отсчета магнита на заряды в контуре действует сила Лоренца, а в системе контура электрическая сила, причем силы должны быть равны:

(2)

Здесь есть скорости магнита в системе контура и скорость контура в системе магнита. Формула (2) показывает, что в системе контура возникает электрическое поле, циркуляция которого и будет равна ЭДС. Детальный анализ показывает, что и в этом случае ЭДС определяется формулой (1). Итак, мы приходим к выводу: при изменении магнитного потока через контур в внем возникает ЭДС, определяемая формулой

(3)

Это и есть закон электромагнитной индукции (закон электромагнитной индукции Фарадея). Знак минус в формуле перед производной означает, что возникающий в результате ЭДС индукционный ток направлен так, что его магнитное поле препятствует изменению магнитного потока.

К еще более фундаментальному выводу мы приходим, если внимательно проанализировать возникновение ЭДС путем перехода в движущуюся относительно магнита систему отсчета. Рассмотренные нами ранее формулы преобразования полей

(4)

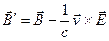(5)

Имеют общий характер. Именно они позволяют утверждать, что изменяющееся магнитное поле порождает электрическое поле, циркуляция которого не равна нулю. Такое поле называется вихревым. Переменное магнитное поле порождает вихревое электрическое поле в пространстве, безотносительно наличия контура с током. Если записать соотношене (3) для произвольного контура

(6)

Последнее рассуждение называется максвелловской трактовкой явления электромагнитной индукции.

Рассмотрим теперь вопрос об энергии токов, которая называется магнитной энергией. Ход рассуждений будет примерно такой же, как и при рассмотрении энергии электрических зарядов и энергии электрического поля. Рассмотрим сначала одиночный замкнуты виток. Пусть в начальный момент сила тока в нем равна нулю. Создадим и будем наращивать в нем ток. В результате появится переменное магнитное поле, переменный поток магнитного поля через виток и ЭДС, которая будет препятствовать наращиванию тока. Совершаемая внешними сиоами работа будет равна

(7)

где - магнитная энергия. Определим коэффициент индукцию контура (точнее коэффициент самоиндукции) с током соотношением

(8)

Тогда из (7) получаем

(9)

Формула (9) также может рассматриваться (наряду с формулой (8)) как определение коэффициента самоидукции. Теперь обобщим результат на случай произвольного число контуров (аналог энергии системы зарядов). Для бесконечно малой работы против сил самоиндукции

Для простоты будем наращивать ток синхронно . Тогда для магнитной энергии получаем выражение

(10)

Аналогично (8) определим коэффициенты взаимной индукции соотношениями

(11)

что для магнитной энергии дает формулу

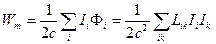(12)

Мы представили магнитную энергию токов как объектов, взаимодействующих силами Ампера. Это соответствует взаимодействию на расстоянии. Для интерпретации этой энергии как энергии магнитного поля получаем выражения (в скобках выражение для магнетиков, смотри приложение к лекции):

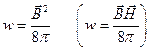(13)

Итак, мы с вами в разных разделах уже встречались со следующими уравнениями

(14)

Первое уравнение –выражает факт отсутствия магнитных зарядов в природе, второе –закон электромагнитной индукции, третье –теорему Гаусса в дифференциальной форме, четвертое теорему о циркуляции для напряженности магнитного поля в дифференциальной форме. И плотность заряда и плотность тока учитывают только свободные заряды. Мы также знаем, что должен выполняться фундаментальный закон – закон сохранения заряда

(15)

Но, взяв дивергенцию от четвертого уравнеия (14), мы получим

что возможно, только при . Следовательно, уравнения (14) непригодны для описания задач с переменной по времени плотностью заряда. Нетрудно увидеть как подправить уравнения (14), чтобы при взятии дивергенции от (14), получалось правильное уравнение непрерывности:

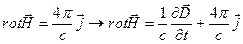
В результате мы приходим к системе уравнений Максвелла в дифференциальной форме

(16)

Добавление члена в правую часть четвертого уравнения(14) эквивалентно добавлению к плотности тока члена , который называется плотностью тока смещения. Необходимость введения тока смещения обосновал Максвелл, он же выписал систему уравнений (16), которая описывает любое электродинамическое явление. К необходимости введения такого члена можно подойти и путем анализа некоторых экспериментальных ситуаций. Разобрать две из них: заряженный шар в проводящей среде, разрядка плоского конденсатора.

Уравнения Максвелла могут быть записаны и в дифференциальной форме. Для этого их нужно проинтегрировать по произвольному объему или поверхности и воспользоваться формулами Остроградского-Гаусса и Стокса. В результате стандартных процедур получаем уравнения

(17)

Формулы (16,17) дают уравнения Максвелла в веществе. Плотности заряда и плотности тока относятся к свободным зарядам и свободным токам. К ним надо еще присоединить материальные уравнения дающие связь напряженностей с индукциями, которые в простейшем случае имеют вид

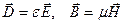(18)

Для вакуума уравнения получаются совсем просто :

(19)

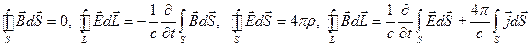(20)В

уравнениях (19,20) плотности заряда и плотности тока включают все заряды и все токи.

Приложение1. Вывод выражения для плотности магнитной энергии.

Сила взаимодействия двух витков с током равна (лекция 7).

(П1)

Для простоты обозначаем 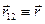и записываем выражение для потенциальной энергии как

(П2)

При интегрировании по первому контуру интеграл от первого слагаемого дает нуль (контур замкнут), а интеграл по второму контуру равен

(П3)

Переходим от локализованных к плотностям токов, к интегрированию по объемам (что означает суммирование по крнтурам) и вводим векторный потенциал

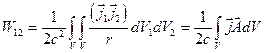(П4)

При этом мы учли множитель так как при суммировании каждая пара учитывается дважды. Используем уравнения (теорему о циркуляции) и формулы векторного анализа

(П5)

Где интеграл от дивергенции как обычно равен нулю. Откуда видно, что плотность магнитной энергийй (энергии магнитного поля) равна

(П6)

Для магнетиков аналогично получаем выражение (в скобках для сравнения энергия электрического поля)

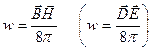(П7)

Дата добавления: 2014-01-07