Похідні вищих порядків та приклади їх обчислення

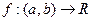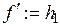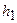Означення 9.5. Нехай функція має похідну на . Якщо функція має похідну 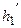, то ця похідна називається похідною другого порядку функції 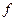, і позначається або , тобто,

.

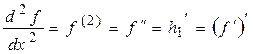Нехай, в свою чергу, функція 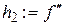має похідну 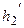на . Тоді 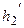називається похідною третього порядку функції 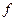і позначається

І так далі. Тобто, якщо функція 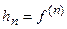має похідну 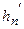на інтервалі то ця похідна називається похідною порядку функції :

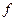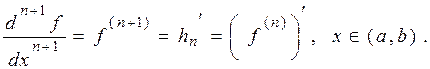
При цьому, саму функцію 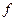називають похідною нульового порядку, а - першого порядку.

Приклад 9.4. а) Якщо, то

.

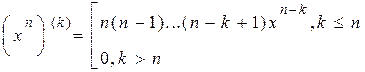б)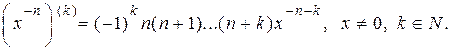

в)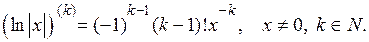

Доведення: Застосуємо метод математичної індукції. Нехай 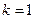. Тоді твердження 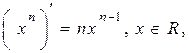за доведеним раніше вірне.

Припустимо, що твердження вірне для деякого натурального числа , тобто,

Покажемо, що тоді твердження вірне і для натурального числа . Дійсно,

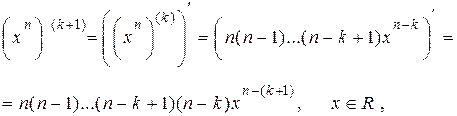
що і потрібно було довести при . Якщо, , то

Тому, при маємо , і, отже, всі наступні похідні теж рівні нулю:

Аналогічно доводяться і твердження б) та в).

Приклад 9.5. Нехай Тоді,

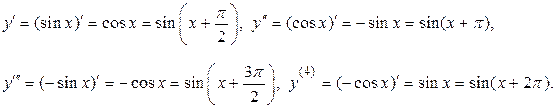
Таким чином, похідні функції 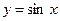періодично повторюються (через чотири порядки), або можна довести (наприклад, методом математичної індукції), що

Аналогічно,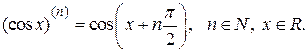

Дата добавления: 2014-01-07