Похідні вищих порядків для добутку функції

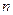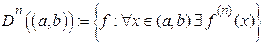Означення 9.5. Будемо називати класом раз диференційованих на інтервалі функцій множину: , і, відповідно, класом 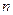раз неперервно диференційованих функцій множину . У означенні відповідних класів для замкненого відрізку 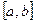будемо додатково вимагати відповідно існування та існування і неперервність похідних зправа в лівому кінці та зліва в правому кінці відрізка 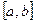, тобто

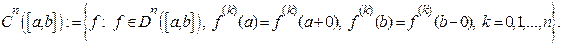Розглянемо питання про похідну вищих порядків добутку функцій.

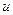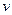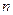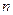Теорема 9.3 (Про формулу Лейбніця). Нехай функції і мають похідні до -го порядку включно на інтервалі . Тоді існує похідна -го порядку на від добутку цих функцій 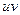, і при цьому виконана рівність

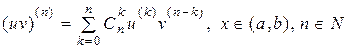(9.6).

Доведення. Застосуємо метод математичної індукції. Очевидно, при 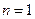формула (9.6) справджується. Дійсно,

Припустимо, що формула (9.6) має місце для деякого натурального числа . Покажемо, що тоді твердження теореми справедливе і для наступного натурального числа . Дійсно,

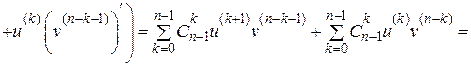
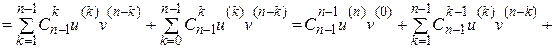
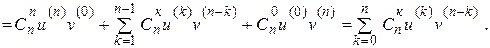
При цьому було використано такі тотожності:

Доведення теореми завершено.

Приклад 9.6. Обчислимо , якщо .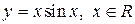

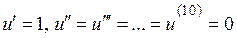Покладемо . Тоді , і

. Отже, за формулою Лейбніца маємо:

Дата добавления: 2014-01-07