Асимптоти графіка функції

Лекція № 11.

Означення 11.1. а) Пряма 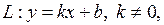називається похилою

асимптотою графіка 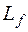функції 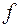на 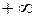або на 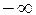, якщо 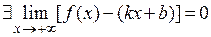, або, відповідно, 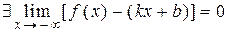. б) Пряма 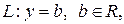називається горизонтальною асимптотою на 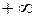або

на 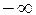графіка 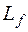функції 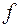, якщо ,

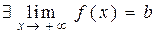або, відповідно, .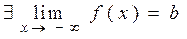

в) Прямя 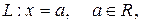називається вертикальною асимптотою графіка 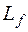функції 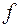, якщо існують границі .

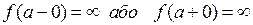Теорема 11.1 (Про необхідні і достатні умови існування похилої асимптоти). Графік функції 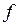має похилу асимптоту 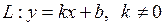на 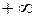тоді і тільки тоді, коли існують границі: (11.1).

Доведення. 1) Достатність. Нехай існують скінчені границі (11.1), тоді за теоремою 5.4 про збереження арифметичних операцій при взятті границі існує границя функції:

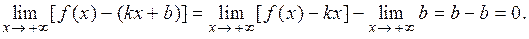
Отже, згідно означення 11.1, пряма 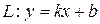є похилою асимптотою графіка функції 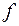на .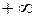

2) Необхідність. Нехай 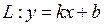є похилою асимптотою графіка функції 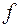на 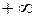. Тоді, згідно о значення 11.1, за теоремою 5.4 про збереження арифметичних операцій при взятті границі та за теоремою 5.9 про класичні границі функцій на 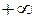,існує границя

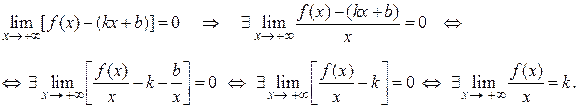Аналогічно, за теоремою 5.4 про збереження арифметичних операцій при взятті границі, маємо:

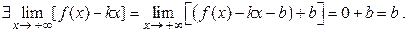Теорему доведено.

Зауваження 11.1. Аналогічне твердження справедливе і для похилої асимптоти на .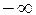

Теорема 11.2 (Про достатні умови існування похилої асимптоти ). Нехай графік функції 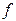має похилу асимптоту на 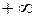(або на 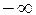). Тоді,

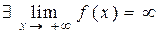(або ).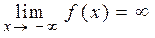

Доведення. Нехай за умовою теореми існує похила асимптота 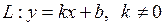на плюс нескінченності. Тоді, за теоремою 11.1 слідує, що існує скінчена відмінна від нуля границя 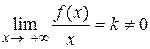. Отже,, за теоремою 5.4 про збереження арифметичних операцій при взятті границі, маємо:

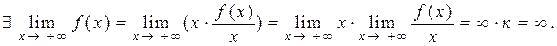
Аналогічно доводиться теорема і у випадку існування асимптоти на лівому кінці числової осі. Доведення закінчено.

Наслідок 11.1. 1) З одного боку числової осі, тобто на 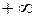або на 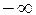, може існувати асимптота тільки одного типу: або похила, або горизонтальна.

2) Якщо функція 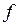неперервна на 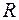, то її графік не має вертикальних асимптот. Якщо пряма 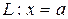є вертикальною асимптотою графіка функції 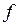, то 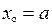є точкою розриву другого роду функції .

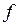Приклад 11.1. Знайти асимптоти графіка функції: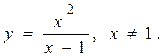

Розв’язання. 1) Легко бачити, що точка 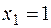є точкою розриву другого роду. Дійсно, легко обчислити границі 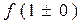діючи формально:

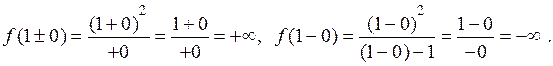
Тому, згідно о значення 11.1, пряма 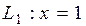є вертикальною асимптотою графіка функції .

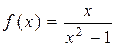2) Обчислимо границю функції 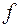на :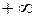

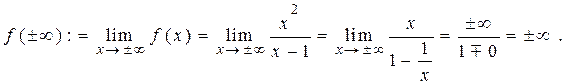
Отже, горизонтальних асимптот немає, але,можливо, існують похилі асимптоти.

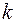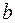3) Знайдемо значення параметрів і , за теоремою 11.1 слідує:

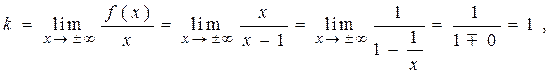
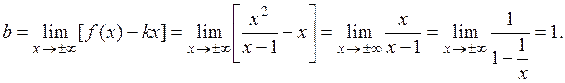
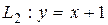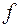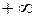Таким чином, пряма є похилою асимптотою графіка функції на і 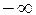, тобто на лівому і правому кінці числової осі .

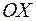Відповідь: 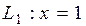- вертикальна асимптота; 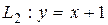похила асимптота на .

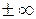Дата добавления: 2014-01-07