Расчет статистических характеристик по сгруппированным данным

Класс x, %	Частота n i	Номер класса xi	Произведения	Сумма частот S ni
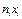
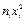
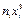
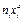
30-32		-5	-10		-250
32-34		-4	-24		-376
34-36		-3	-27		-243
36-38		-2	-28		-112
38-40		-1	-20		-20
40-42
42-44
44-46
46-48
48-50
50-52
52-54
54-56
Cумма		–					–
Среднее	–	–	0,56	6,80	14,33	132,30	–
Моменты	–	–	m 1	m 2	m 3	m 4	–

Между формулами (2.14) и (2.17) имеются различия. Так, в формулах (2.17) появляется размер классов h, играющий роль масштабного множителя, и поправки Шеппарда, которые возник ли из-за того, что внутри классов нивелированы различия между отдельными значениями.

Поправка Шеппарда ко второму центральному моменту – h /12, к третьему – m ₁ h ², к четвертому .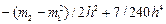

По данным табл.2.5 вычисляем статистические характеристики:

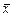= 41 + 0,56×2 = 42,12; m₂ = (6,80 – 0,56² – 1/12)2² = 25,6;

m₃ = (14,33 – 3×6,80×0,56 + 2×0,56³)2³ – 0,56×2² = 23,82;

m₄ = (132,3 – 4×14,33×0,56 +

+ 6×6,80×0,56² – 3×0,56⁴)2⁴ – (6,80 – 0,56)/2×2² +

+ 7/240×2⁴ = 1790,7;

s² = 25,6; s = 5,06; s³ = 129,5; s⁴ = 655,36;

V = 5,06/42,12 = 0,120 = 12,0 %; A = 23,82/129,5 = 0,184;

E = 1790,7/655,36 – 3 = –0,268.

Медиану в сгруппированных данных находят линейной интерполяцией в том классе, где нарастающая сумма частот (последняя графа табл.2.5) переходит через половину общего числа значений n. В рассматриваемом примере из 147 значений средний член имеет порядковый номер (147 + 1)/2 = 74. Следовательно, медиана заключена в классе 40-42, где находятся порядковые номера с 52 по 76. Обозначим начало класса x _н = 40, число значений в классе n_i = 25. Порядковый номер медианы в классе найдем как разность n _т = 74 – 51 = 23.

Тогда медиана

(2.18)

Подставляя данные, получим x _med = 40 + 23/25×2 = 41,84.

Один из приемов нахождения моды основан на параболической интерполяции частот по трем соседним классам, включая класс с максимальной частотой.

В рассматриваемом примере это будут классы 38-40, 40-42, 42-44 с частотами соответственно 20, 25, 21.

Обозначим частоты этих классов n ₁, n ₂, n ₃.

Тогда мода

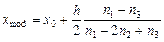, (2.19)

где x ₀ – середина класса с максимальной частотой.

Подставляя численные значения, найдем

.

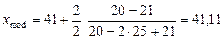Подведем итог расчета статистических характеристик: среднее значение 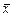= 42,12; медиана x _med = 41,84; мода x _mod = 41,11; дисперсия s² = 25,6; среднеквадратичное отклонение s = 5,06; коэффициент вариации V = 12,0 %; асимметрия A = 0,184; эксцесс E = –0,268.

Геологические приложения одномерной статистической модели

Дата добавления: 2014-01-07