Виды трехмерного моделирования

Геометрические трехмерные модели делятся на три вида: каркасные (проволочные), поверхностные и твердотельные (сплошные).

Каркасная модель полностью описывается геометрическими объектами первого порядка – линиями и ребрами. Такие модели применяются, как правило, для задания объектов, представляющих собой замкнутые многогранники произвольной формы, ограниченные плоскими гранями, или объекты, получаемые перемещением образующей, которая фиксируется в некоторых положениях. Модель в этом случае описывается координатами вершин многогранника с указанием связей между ними, т.е. ребер. Пример каркасной модели представлен на рис. 18.1.

Каркасное моделирование представляет собой моделирование самого низкого уровня и имеет ряд серьезных ограничений, большинство из которых возникает из-за недостатка информации о гранях, заключенных между линиями, и невозможности выделить внешнюю и внутреннюю области изображения твердого объемного тела.

Рис. 18.1

Однако каркасная модель требует гораздо меньше памяти, чем другие модели, и может быть использована для построения изображений объектов, имеющих простые формы.

Поверхностная модель определяется с помощью точек, линий и поверхностей. Поверхностное моделирование позволяет распознавать и изображать сложные криволинейные грани и обеспечивать способность распознавать особые построения на поверхности, например отверстия (рис. 18.2).

Рис. 18.2

Методы поверхностного моделирования применяются в областях, где проектируются динамические поверхности, т.е. поверхности, взаимодействующие с внешней средой. Таким образом, поверхностное моделирование можно рассматривать как моделирование более высокого уровня, чем каркасное. Создаваемые при этом модели являются более гибкими и многофункциональными.

Несмотря на целый ряд достоинств метода поверхностного модели­рования, его применение ограничено из-за недостатков и, прежде всего, из-за сложности процедуры удаления невидимых линий и отображения внутренних областей.

Твердотельная модель описывается в терминах того трехмерного объема, который занимает определяемое моделью тело. Тела описываются точками, кривыми и поверхностями и обладают определенными общими свойствами, позволяющими оперировать ими как объектами. При моделировании тел строятся поверхности, отделяющие занимаемую ими часть пространства в зависимости от способа их описания. Этот способ моделирования представляет собой самый современный и наиболее мощный из трех методов моделирования и является единственным средством, обеспечивающим полное однозначное описание трехмерной геометрической формы.

Методы твердотельного моделирования, используемые в современных CAD системах, делятся на методы:

• конструктивного представления (Constractive Solid Geometry или CGS), основанный на использовании базовых объемных примитивов, каждый из которых характеризуется формой, размерами, точкой привязки и ориентацией. К таким примитивам, как правило, относят прямоугольную и треугольную призмы, сферу, цилиндр, конус и тор. Над примитивами и полученными из них телами можно выполнять различные операции, в первую очередь булевы операции – объединения, вычитания и пересечения тел над множествами точек пространства, находящимися внутри тел (рис.18.3).

• граничного представления (Bounded representation или B-rep), основанный на сохранении в памяти компьютера всех тех элементов, которые создают границы объекта – поверхности и указатели пересечения поверхностей. Этот метод дает возможность выполнять над телами множество операций, сохраняя при этом единый способ их внутреннего устройства, связь элементов друг с другом. Представление тел с помощью границ позволяет моделировать объекты произвольной формы и сложности.

• пространственного заполнения или ячеечный (Faceted representation или Faceted). При использовании этого метода ограниченный участок пространства, охватывающий весь моделируемый объект, считается разбитым на большое число дискретных кубических ячеек. В простейшем случае размеры куба равны единице измерения длины. Моделирующая система записывает информацию о принадлежности или не принадлежности каждого куба телу объекта. Структура данных представляется трехмерной матрицей.

Твердотельные примитивы	Булева операция
объединения (АÈВ)	вычитания (А-В)	пересечения (АÇВ)
	Результатом операции объединениядвух тел является тело, которое содержит точки, принадлежащие внутреннему объему или первого или второго тела	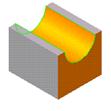Результатом вычитания двух тел является тело, которое содержит точки, принадлежащие внутреннему объему первого, но не принадлежащие внутреннему объему второго тела	Результатом операции пересечениядвух тел является тело, которое содержит точки, принадлежащие внутреннему объему, как первого, так и второго тела

Рис. 18.3

Дата добавления: 2014-01-07