Негауссова статистика

Классическая статистика

ДИНАМИЧЕСКИХ СИСТЕМ

СТОХАСТИЧЕСКОЕ ОПИСАНИЕ

И ДЕТЕРМИНИРОВАННЫЙ)

ДВА ПОДХОДА К ОПИСАНИЮ ДИНАМИЧЕСКИХ СИСТЕМ МНОГИХ ЧАСТИЦ (СТОХАСТИЧЕСКИЙ

ЛЕКЦИЯ 13.

МАТЕМАТИКА И ОБЩЕСТВО:

1. Два подхода к описанию динамических систем многих частиц (стохастический и детерминированный).

2. Стохастическое описание динамических систем

3. Описание динамических систем геометризированной теорией множеств.

4. Фрактальная геометрия динамических систем.

5. Фрактально-топологическая (фазовая) модель товарно-денежного хозяйства.

В математике природа точек (точки-частицы) не играет никакой роли и отличающиеся по природе реальные системы частиц (физические, биологические, экономические и т.д.) могут рассматриваться как проявления одного и того же объекта – изоморфизмы (взаимно однозначные отображения множеств, сохраняющие их структурные свойства) или гомеоморфизмы (топологически эквивалентные пространства). Кажущееся абстрактным понятие изоморфизма является просто математическим выражением идеи моделирования явлений из одной области (например, тепловых) явлениями из другой области (например, электрических).

Единую математическую природу имеют такие, на первый взгляд, совершенно разные процессы, как «броуновское» движение микрочастиц в жидкости, рассеяние тепла в веществе и движение стоимости ценных бумаг.

Математические модели разделяются на стохастические (вероятностные), включающие случайные компоненты, структуры, функции или последовательности и т.п., то есть удовлетворяющие статистическим законам, и детерминированные, которые не содержат таких компонентов.

В настоящее время в прикладной науке господствуют стохастические модели, в которых вероятность распределения событий описывается симметричной «колоколообразной» кривой Гаусса (классическая статистика, типичный пример – «броуновское» движение). Эта кривая базируется на принципах относительного «равноправия», «равнозначности», «равноценности», «однородности» событий (каждое событие вносит вклад в общую сумму, но ни одно из них не определяет статистический результат). В этом случае независимо от природы и размера элементов, а также от природы ресурса систем плотность вероятности распределения для их переменных состояния x подчиняется “нормальному” (“стандартному”, “экспоненциальному”) рпспределениюгде постоянные a и b положительны. Особенности конкретной системы учитываются абсолютными величинами a и b, а также тем, какая конкретно величина подразумевается под переменной x. Например, 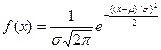. При этом основными характеристиками являются: μ – среднее значение x; σ – стандартное отклонение (средне квадратическое отклонение – ширина разброса всех x вокруг μ). Подстановка конкретных величин, а также учет того факта, что x может зависеть от a, позволяет, например, преобразовать уравнение в основное уравнение статистической физики (канонический ансамбль Гиббса).

В статистике независимых событий предыдущее событие не влияет на последующее, а вероятность одновременного появления событий А и В, вероятность появления которых в отдельности больше нуля, соответствует произведению этих отдельных событий. Классическая статистика используется механикой, физикой, химией, биологией и социально-экономическими науками, включая экономику, то есть для описания систем саиой различной природы: размеров капелек воды в облаках и размеров частиц золотоносных россыпей, кинетической энергии молекул газа и звёзд, термического шума, колебаний цен в условиях совершенной конкуренции и т.д. Например, в основе широко известной гипотезы эффективного рынка лежит именно модель случайного длуждания, предложенная Луи Башелье. Соглесно ей последовательные изменения цен статистически независимы и колеблются вокруг “объективной” цены, которая определяется консенсусом большого числа рационально мыслящих участников рынка.

Известна также форма статистики, в которой плотность вероятности распределения описывается несимметричной кривой с максимумом, а убывание переменной подчиняется степенному (гиперболическому) закону типа . Например, статистика Коши, в которой функцией приведенной плотности вероятности является . Системы, которые не подчиняются закону Гаусса широео распространены в природе, технике и обществе.

Одним из первых степенной закон распределения в экономике описал итальянский социолог и экономист В. Парето в конце XIX столетия. Он установил, что распределение доходов во всех странах и во все эпохи не подчинялось «нормальному» закону. Доля богатых, это значит имеющих доход выше определенного уровня (u), описывается формулой , где m – минимальный доход, 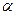- параметр Парето. В логарифмических осях (дважды логарифмический график) формула описывает прямую линию с наклоном 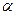. Парето получил наклон, равный 3/2, который свидетельствует о том, что основная масса общественного богатства сконцентрирована в руках богатого меньшинства (чем менше нвклон, тем более равномерно распределены доходы; равномерному распределению соответствует . Согласно формуле Парето в существующей экономике деньги порождают деньги (возможность стать богатым больше у богатого человека), власть порождает власть. Показатель 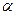в формуле Парето – это “количественное выражение несправедливости в обществе”.

Дважды логарифмический график является также характерным для распределения населенных пунктов по численности населения (распределение Саймона, показатель 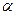близок к 2), научных работников по количеству опубликованных ими работ (распределение Лотка, показатель 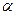колеблется между 2 и 3), стоимости ценных бумаг на современных финансовых рынках (распределение Мандельброта), частоты встречаемости слов в литературном и разговорном языках (распределение Ципфа), организмов по размерам в разных экосистемах (почвенной фауны, океанского зоопланктона и др.), количества землетрясений по их магнитуде, излучаемой при разрушении материалов энергии, величины упругих импульсов и размеров получаемых при дроблении твердых тел частиц, количества метеоритов по массе и т.д. Согласно Фёрстеру дважды логарифмическая линейная регрессия имеет место для зависимостей “сложность-устойчивость”элементов как живых(например, организмы), так и неживых (например, атомы) неоднородных систем. В первом случае она положительная, а во втором – отрицательная.

Основоположник фрактальной геометрии Мандельброт показал, что гиперболические распределения – «ближайшие родственники фракталов» (самоподобных геометрических структур), что они статистически самоподобны (масштабно-инвариантны) и назвал такую статистику фрактальной. Им введено понятие фрактальной размерности пространства вероятностей (роль размерности играет показатель степени). Им введено понятие фрактальной размерности пространства вероятностей. В таких распределениях роль размерности выполняет показатель 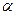. Он пришел к выводу о том, что имеет место несколько форм «случайности» и попробовал отождествить их с агрегатными (твердым, жидким и газообразным) состояниями материи. Согласно его мнению, теория вероятностей выявляет «аналогии с теорией вещества», которые выводятся «из одних и тех же принципов и используют одни и те же концепции – например, такие, как температура и давление». Он подчеркивает, что “если ввести в математику отличия между состояниями случая, то это только дополднит математику, не изменяя её. Зато в корне перевернет интерпретацию этих самых состяний». «Понятие случай, - отмечает он, - выступает в науке в самых разных формах, и мы только выиграем, если допустим, что случай может находиться нескольких состояниях», «три состояния материи – твердое, жидкое и газообразное – известны уже давно, из математического аппарата фрактальной геометрии вытекает аналогичное различие между тремя состояниями случайности – мягкая, медленная и бурная».

Анализ экспериментальгых стохастическтх данных, полученных разными науками (механикой, физикой, химией, биологий, социологий, экономикой и т.д.), показывает, что они в основном стремяться к распределениям, описываемым именно зеконами двух типов: “нормальным” законом (распределение Гаусса, равнозначные события) и дважды логарифмическим (билогарифмическим) законом (степенной закон, неравнозначные события). Согласно Мандельброту рассматриваемые два типа распределений – это “две крайности”, которые целым спектром других “членов семьи” связывает распределение Леви: .

Распределение Леви имеет четыре ключевые переменные, которые определяют окончательую форму кривой (Гаусса, Парето и др.): δ – параметр “местоположения”, γ – параметр масштаба (определяет величину общей вероятности), β – параметр асимметричности (при β = 0 кривая симметрична), α – параметр, который определяет “толщину хвостов”. Когда α = 2, а β = 0, то распределение Леви описывает стандартную кривую Гаусса, при α = 1, а β = 0 - кривую Коши с очень “толстыми хвостами”.

В мире Гаусса события (ошибки) распределены как размеры почти одинаковых песчинок (однородные системы). Взгляд Коши на мир совершенно другой. В мире Коши события (ошибки) представляют собой вроде смеси песчинок, гравия, валунов и гор (неоднородные системы).

Следует отметить, что впервые «неожиданную» аналогию между свойствами вещества, а точнее (рассеянием, или диффузией тепла в веществе) и колебаниями цен облигаций заметил французский ученый Башелье (1900 г.). Он применил для описания колебаний цен облигаций уравнения рассеяния тепла Фурье, то есть адаптировал уравнения одной науки (физики) к потребностям другой науки (финансов).

Более широкая идея называть преобразующее природу человечество «живым веществом» принадлежит В.И. Вернадскому. Субъекты хозяйствования часто называют «молекулами», «атомами», «химическими элементами» (например, лауреат Нобелевской премии по экономике Коуз, социолог Питирим Сорокин и др.).

Дата добавления: 2014-01-07