Геометризированной теорией множеств

ОПИСАНИЕ ДИНАМИЧЕСКИХ СИСТЕМ

В математике в общем случае объект или процесс описывается системой n интегро-дифференциальных уравнений, определенной в пространстве R^N с координатами :

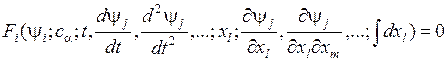(1)

Переменные x_l и t рассматриваются как пространственные и временные координаты. Решения 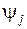, описывающие состояния системы, называются переменными состояния; 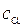– управляющими параметрами.

Решение системы уравнений (1) является сложной задачей. Поэтому ее упрощают, ограничиваясь, во-первых, системой уравнений в частных производных, не содержащих пространственных производных, во-вторых, предполагая, что она не зависит от пространственных координат, и, наконец, считая, что она содержит производные по времени не выше первого порядка, которые входят в упрощенную функцию специальным («каноническим») образом: .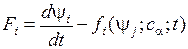

Систему уравнений 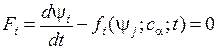(2) называют динамической системой.

Если функции в уравнениях (2) не зависят от времени, то такая система называется автономной динамической системой:

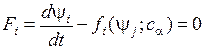
В случае консервативных систем возможно значительное упрощение системы уравнений (1):

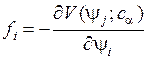
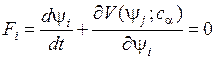, (3)

Эту систему называют градиентной (потенциальной) динамической системой.

Наибольший интерес представляет изучение состояний равновесия градиентных систем:

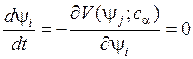, (4)

Именно такого рода динамические системы в основном изучаются в настоящее время.

Потенциальные системы многих частиц (частицы движутся несвободно) – «вязкие» системы, в которых пропорциональна приложенной силе скорость движения частицы (системы Аристотеля), а не ее ускорение (системы Ньютона). Это нелинейные системы.

Нелинейные системы описываются нелинейными дифференциальными уравнениями, которые имеют несколько решений (корней, радикалов) и, соответственно, все нелинейные системы имеют несколько стационарных (установившихся) состояний, а протекающие в них процессы являются ветвящимися.

В нелинейных системах наблюдаются качественные, включая скачкообразные, изменения свойств при плавном изменении величины воздействующих на них факторов.

Наибольших успехов в изучении нелинейных динамических систем достигла геометризированная теория множеств - топологическая теория бифуркаций критических точек потенциальных функций (теория катастроф).

Топология – раздел математики, изучающий наиболее общие свойства пространств (фигур), сохраняющихся (инвариантных) при непрерывных преобразованиях (без разрывов и склеивания). Это наиболее общая геометрия.

Топологическое пространство – имеющее структуру множество элементов произвольной природы, называемых точками (структурированное множество).

Фазовое пространство – пространство, элементами которого являются фазовые точки – совокупности, значений параметров, определяющих состояние системы.

Топологическая динамическая система – непрерывная динамическая система.

Для систем с одной переменной состояния x функции катастроф (первые члены разложенной в ряд потенциальной функции, которые определяют качественное поведение системы) при уменьшении потенциальной энергии, записываются в виде:

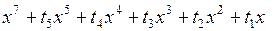(катастрофа вигвам),

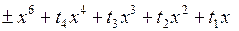(катастрофа бабочка),

(катастрофа ласточкин хвост),

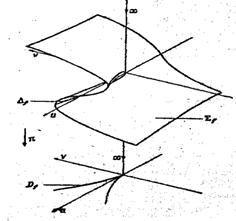
(катастрофа сборка),

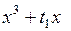(катастрофа складка),

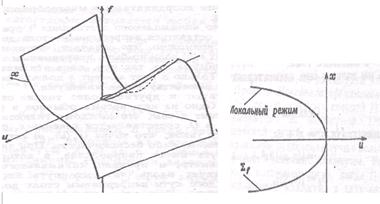
где высший член называется ростком катастрофы, а сумма остальных членов – возмущением (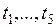– управляющие коэффициенты).

Потенциальная функция Критические точки

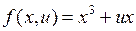
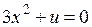
Рис. 13.1. Катастрофа «складка»

Потенциальная функция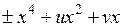

Критические точки и их проекция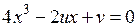

Рис. 13.2. Катастрофа «сборка»

Дата добавления: 2014-01-07