Расчет поля плоского конденсатора

Для расчета электрических полей

Применение теоремы Гаусса

Плоский конденсатор состоит из двух пластин близко расположенных. Пластины имеют равные по величине заряды противоположных знаков. Заряды равномерно распределены по площади пластин, т.е. , где S – площадь пластины конденсатора, σ – поверхностная плотность заряда. (Рис.13)

Следовательно, поле конденсатора это результат суперпозиция полей, которые созданы каждой из пластин:

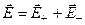или в проекции на ось Х: 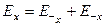. (8.26)

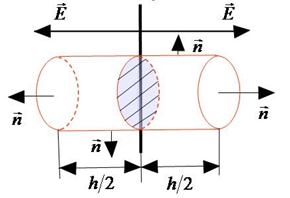Рассчитаем поле каждой пластины, пользуясь теоремой Гаусса. Для этого выберем произвольную замкнутую поверхность в виде цилиндра. Ось цилиндра расположим перпендикулярно пластине конденсатора, а цилиндр расположен симметрично заряду пластины. Точка, в которой рассчитывается поле, находится на одном из оснований цилиндра (Рис. 14).

Рассчитаем поток напряженности через поверхность цилиндра, т.е. через два его основания и боковую поверхность:

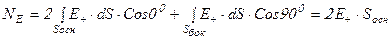(8.27)

Теперь определим алгебраическую сумму зарядов, находящихся внутри цилиндрической поверхности, и поделим её на :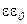

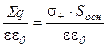(8.28)

Согласно теореме Гаусса приравняем уравнения (8.27) и (8.28) и выразим напряженность поля пластины:

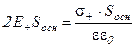
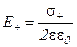(8.29)

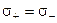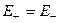Из уравнения (8.29) видно, что поле пластины не зависит от положения точки относительно пластины, т.е. поле пластины однородное. Кроме того, площади пластин, их заряды по величине одинаковы, следовательно, и . Учитывая это, найдем напряженность поля конденсатора в областях пространства 1, 11, 111 (Рис.13). В областях 1 и 111 напряженность поля равна нулю, а в области 11 получаем, пользуясь уравнением (8.29):

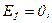
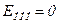(8.30)

Полученные результаты позволяют сформулировать вывод. Поле плоского конденсатора однородное и сосредоточено между пластин конденсатора.

Чтобы закончить расчет поля конденсатора необходимо определить во всех точках этого поля его потенциал. Воспользуемся тем, что характеристики поля, напряженность и потенциал, связаны между собой уравнением (8.11) -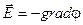. Запишем это уравнение для одномерного случая и рассмотрим поведение потенциала в областях пространства 1, 11, 111.

или 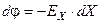(8.31)

В областях 1 и 111 , следовательно, потенциал поля по уравнению (8.31) в этих частях пространства будет величиной постоянной -и .

Рассчитаем потенциал в области 11, когда координата Х изменяется в пределах от 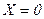до 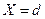, взяв неопределенный интеграл и учитывая, что :

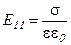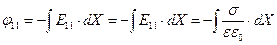
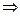
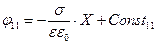. (8.32)

Из уравнения (8.32) видно, что при изменении Х потенциал поля между пластинами конденсатора уменьшается по линейному закону, следовательно, 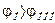. Определим, насколько изменяется потенциал поля между пластинами, учитывая, что потенциал функция непрерывная, в отличие от напряженности поля.

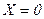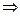
В точке имеем тогда и уравнение (8.31) принимает вид:

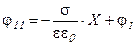(8.33)

В точке 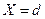имеем и тогда уравнение (8.31) принимает вид:

(8.34)

Из последнего уравнения находим, насколько изменяется потенциал поля между пластинами конденсатора:

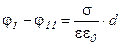
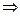
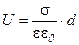(8.35)

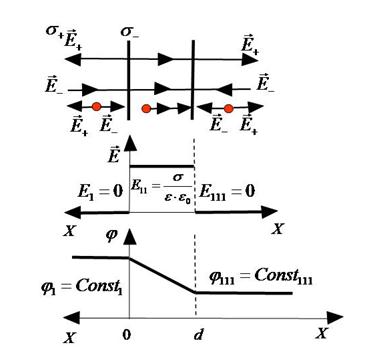Представим результаты расчета поля конденсатора на графике (Рис.15):

Дата добавления: 2014-01-07