Лекция № 7. Вопрос 8. Прирост (уменьшение) оборотных средств, источники его покрытия

Вопрос 8. Прирост (уменьшение) оборотных средств, источники его покрытия

Сопоставление совокупной потребности в собственных оборотных средствах на конец и начало планируемого периода определяет прирост или уменьшение собственных оборотных средств. Прирост оборотных средств находит отражение в финансовом плане и требует определения источников его покрытия. Такими источниками могут быть:

♦ излишек оборотных средств на начало года;

♦ неиспользованная прибыль предприятия;

♦ прирост кредиторской задолженности, постоянно находящейся в обороте предприятия (устойчивые пассивы), т. е. приравненные к собственным источники;

♦ эмиссия ценных бумаг;

♦ прочие источники.

Излишек или недостаток оборотных средств определяется путем сопоставления фактического наличия собственных оборотных средств по балансу с потребностью в них. Фактическое наличие собственных оборотных средств определяется по следующему расчету:

Итог раздела III баланса + строки 640, 650 раздела V баланса – (Итог раздела I – раздел IV)

Излишек оборотных средств означает омертвление средств в излишних запасах товарно-материальных ценностей, что замедляет оборачиваемость оборотных средств; увеличивает расходы, связанные с хранением этих запасов.

Основными причинами образования сверхнормативных запасов могут быть:

♦ по производственным запасам – излишние и неиспользуемые материалы на складе, неравномерное поступление материальных ресурсов,;

♦ по незавершенному производству – удорожание себестоимости в результате несоблюдения технологии производства, перерасход материальных ресурсов,;

♦ по готовой продукции – низкое качество, сбои в отгрузке, изменение ситуации на рынке сбыта.

Недостаток оборотных средств приводит к сбоям в производственном процессе в связи с невозможностью своевременно пополнять производственные запасы, осуществлять расчеты с кредиторами, работниками, банками и т. д. Все это ухудшает платежеспособность предприятия и может привести к банкротству.

Постановка задач нелинейного программирования. Выпуклые и вогнутые функции. Основная задача выпуклого программирования. Метод Лагранжа решения задач нелинейного программирования.

Задачи нелинейного программирования. Экономическая и геометрическая интерпретации задачи нелинейного программирования.

В общем виде задача нелинейного программирования состоит в определении максимального (минимального) значения функции

f (x₁, x₂, …, x_n) (1)

при условии, что ее переменные удовлетворяют соотношениям

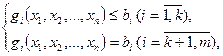(2)

где f и g_i — некоторые известные функции n переменных, а b_i — заданные числа.

Здесь имеется в виду, что в результате решения задачи будет определена точка Х*= (х* ₁; х* ₂; ...; x*_n), координаты которой удовлетворяют соотношениям (2) и такая, что для всякой другой точки Х= (х ₁; х₂;...; х_n), удовлетворяющей условиям (2), выполняется неравенство f (х* ₁; х* ₂; ...; x*_n) ≥f (х ₁, х₂,..., х_п) [ f (х* ₁; х* ₂; ...; x*_n) ≤f (х ₁, х₂,..., х_п)].

Если f и g_i — линейные функции, то задача (1), (2) является задачей линейного программирования. Если f — нелинейная функция, то задача (1), (2) является задачей нелинейного программирования.

Соотношения (2) образуют систему ограничений и включают в себя условия неотрицательности переменных, если такие условия имеются. Условия неотрицательности переменных могут быть заданы и непосредственно.

Задача. Найти максимальное значение функции

f = x ₂- x ₁²+6 x ₁ (3)

при условиях

(4)

(5)

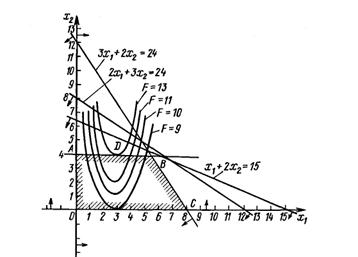
Решение. Так как целевая функция (3) нелинейная, то задача (3) — (5) является задачей нелинейного программирования. Областью допустимых решений данной задачи является многоугольник ОАВС (рис. 1). Следовательно, для нахождения ее решения нужно определить такую точку многоугольника ОАВС, в которой функция (3) принимает максимальное значение. Построим линию уровня f = x ₂- x ₁²+6 x ₁= h, где h — некоторая постоянная, и исследуем ее поведение при различных значениях h. При каждом значении h получаем параболу, которая тем выше отдалена от оси Ох ₁, чем больше значение h (рис. 1). Значит, функция f принимает максимальное значение в точке касания одной из парабол с границей многоугольника ОАВС. В данном случае это точка D (рис.1), в которой линия уровня f = x ₂- x ₁²+6 x ₁=13 касается стороны АВ многоугольника ОАВС. Координаты точки D можно найти из системы уравнений

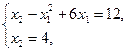(6)

Решая эту систему, получим х ₁*=3; х ₂*=4. Итак, f _max=13 при Х *=(3; 4).

Рис.1

Как видим, в задаче (3) — (5) точка максимального значения целевой функции не является вершиной многоугольника решений. Поэтому процедура перебора вершин, которая использовалась при решении задач линейного программирования, неприменима для решения данной задачи.

Задача. Найти максимальное и минимальное значения функции

f =(х ₁-3)²+(x ₂-4)² (7)

при условиях

(8)

x ₁, x ₂ ≥ 0. (9)

в точке D. Из уравнения прямой x ₂=10 x ₁-8 видим, что ее угловой коэффициент в точке D равен 10. Угловой же коэффициент касательной к окружности в точке D определим как значение производной функции х ₂ от переменной x ₁ в этой точке. Рассматривая x ₂ как неявную функцию переменной х ₁ и дифференцируя уравнение окружности, получим 2(x ₁-3)+2(x ₂-4) x ^'₂=0, откуда x ^'₂=-(x ₁-2)/(x ₂-4).

Решение. Областью допустимых решений задачи (7) — (9) является треугольник АВС (рис. 2). Полагая значение целевой функции (7) равным некоторому числу h, получаем линии уровня, а именно окружности (х ₁-3)²+(x ₂-4)²= h с центром Е (3; 4) и радиусом . С увеличением (уменьшением) числа h значения функции f соответственно увеличиваются (уменьшаются).

Рис.2

Проводя из точки Е окружности разных радиусов, видим, что минимальное значение целевая функция принимает в точке D, в которой окружность касается области решений. Для определения координат этой точки воспользуемся равенством угловых коэффициентов прямой 10x₁—х₂=8 и касательной к окружности

Приравнивая найденное выражение числу 10, получаем одно из уравнений для определения координат точки Е. Присоединяя к нему уравнение прямой, на которой лежит точка Е, имеем систему

откуда x ₁*=123/101; х ₂*=422/101. Таким образом, f _min=(123/101-З)² + (422/101-4)² =324/101.

Как видно из рис. 2, целевая функция принимает максимальное значение в точке С (2; 12). Ее координаты определены путем решения системы уравнений прямых, на пересечении которых находится точка С. Таким образом, максимальное значение функции f _mах=65.

Задача. Найти максимальное и минимальное значения функции

f =(х ₁-4)²+(x ₂-3)² (10)

при условиях

(11)

x₁, x₂ ≥ 0. (12)

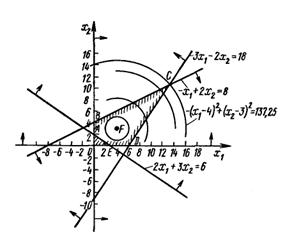
Решение. Областью допустимых решений исходной задачи является многоугольник АВСDЕ (рис. 3), а линиями уровня — окружности (x ₁-4)²+(х ₂-3)²= h с центром Е (4; 3) и радиусом R=.

Из рис. 3 (см. ниже) видно, что целевая функция принимает минимальное значение в точке F (4; 3), а максимальное — в точке С (13; 10,5). Следовательно, f _min=0 и f_тах= 137,25.

Рис.3

Задача. Найти максимальное значение функции

f =3 x ₁+4 х ₂ (13)

при условиях

(14)

x ₁, x ₂ ≥ 0. (15)

Решение. Область решений задачи (13) — (15) изображена на рис. 4. На этом рисунке построены две линии уровня, представляющие собой прямые. Из рис. 4 видно, что максимальное значение целевая функция задачи принимает в точке Е, в которой прямая касается окружности =25. Для определения координат точки Е воспользуемся равенством угловых коэффициентов прямой 3 x ₁+4 х ₂= h (где h —некоторая постоянная) и касательной к окружности в точке Е.

Рис. 4

Рассматривая х ₂ как неявную функцию переменной х₁, почленно дифференцируем уравнение окружности = 25 и получим 2 x ₁+2 x ₂ x ^'₂=0, или x ^'₂=- x ₁/ x ₂.

Таким образом, процесс нахождения решения задачи линейного программирования (1), (2) с использованием геометрической интерпретации включает следующие этапы:

1) Находят область допустимых решений задачи, определяемую соотношениями (2) (если она пуста, то задача не имеет решений).

2) Строят гиперповерхность f (x₁, x₂, …, x_n)= h.

3) Определяют поверхность наивысшего (наинизшего) уровня или устанавливают неразрешимость задачи из-за неограниченности функции (1) сверху (снизу) на множестве допустимых решений.

4) Находят точку области допустимых решений, через которую проходит гиперповерхность наивысшего (наинизшего) уровня, и определяют в ней значение функции (1).

Дата добавления: 2014-01-07