Метод множителей Лагранжа

Рассмотрим частный случай общей задачи нелинейного программирования (1), (2), предполагая, что система ограничений (2) содержит только уравнения, отсутствуют условия неотрицательности переменных и f (х₁, х₂,..., х_п) и g_i (х₁, х_2,…,х_п) — функции, непрерывные вместе со своими частными производными.

f (х ₁, х ₂, ..., х_п) max (min), (16)

g_i (х ₁, х₂,…, х_п) = b_i (i = ). (17)

В курсе математического анализа задачу (16), (17) называют задачей на условный экстремум или классической задачей оптимизации.

Чтобы найти решение этой задачи, вводят набор переменных λ₁, λ₂, …, λ _m называемых множителями Лагранжа, составляют функцию Лагранжа

F (x ₁, x ₂, …, x_n, λ₁, λ₂,…, λ _m) = f (x ₁, x ₂,…, x _n)+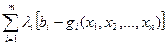, (18)

находят частные производные и и рассматривают систему n + m уравнений

(19)

с п+т неизвестными х ₁, х ₂,..., х _n, λ₁, λ₂,…,λ _m. Всякое решение системы уравнений (19) определяет точку Х=(х ₁⁰, х ₂⁰,..., х_n ⁰), в которой может иметь место экстремум функции f (х ₁, х ₂, ..., х_n). Следовательно, решив систему уравнений (19), получают все точки, в которых функция (16) может иметь экстремальные значения. Дальнейшее исследование найденных точек проводят так же, как и в случае безусловного экстремума.

Таким образом, определение экстремальных точек задачи (16), (17) методом множителей Лагранжа включает следующие этапы:

1) Составляют функцию Лагранжа.

2) Находят частные производные от функции Лагранжа по переменным x_j и λ _i и приравнивают их нулю.

3) Решая систему уравнений (19), находят точки, в которых целевая функция задачи может иметь экстремум.

4) Среди точек, подозрительных на экстремум, находят такие, в которых достигается экстремум, и вычисляют значения функции (16) в этих точках.

Задача. Решим теперь задачу, используя метод множителей Лагранжа. Найдем минимальное значение функции

f =4 x ₁+ x ₁²+8 x ₂+ x ₂² (20)

при условии

x ₁ +x ₂ = 180, (21)

x ₁, x ₂ ≥ 0. (22)

т. е. без учета требования неотрицательности переменных. Для этого составим функцию Лагранжа

F (x ₁, x ₂, λ)=4 x ₁+ x ₁²+8 x ₂+ x ₂²+λ (180- x ₁- x ₂),

вычислим ее частные производные по x ₁, x ₂, λ и приравняем их нулю:

Перенося в правые части первых двух уравнений λ и приравнивая их левые части, получим

4+2 x ₁=8+2 x ₂, или x ₁- x ₂=2.

Решая последнее уравнение совместно с уравнением х ₁+ x ₂=180, находим x ₁*=91 и х ₂*=89, т.е. получили координаты точки D, удовлетворяющей условиям

x ₁, x ₂ ≥ 0. (22)

Эта точка является подозрительной на экстремум. Используя вторые частные производные, можно показать, что в точке D функция f имеет условный минимум. Этот результат и был получен выше.

Следует отметить, что такой же результат мы получим и в том случае, если исследование на условный экстремум функции f сведем к исследованию на безусловный экстремум функции f₁, полученной из f в результате ее преобразований. А именно: если из уравнения связи (21) найдем x ₂=180- х ₁ и подставим это выражение в (20), то получим функцию одной переменной х ₁:

f ₁=4 х ₁+ х ₁²+8(180- х ₁)+(180- х ₁)².

Найдем стационарную точку этой функции из уравнения =4+2 x ₁-8-2(180- x ₁)=0, или 4 x ₁-364=0, откуда x ₁^*=91; x ₂^*=89. Так же как и выше, устанавливаем, что в данной точке функция f имеет минимальное значение.

Задача. Найти точки экстремума функции f=х ₁²+ х ₂² при условии x ₁+ x ₂=5.

Решение. Составим функцию Лагранжа

F(x ₁, x ₂, λ)= х ₁²+ х ₂²+λ (5- x ₁- x ₂),

найдем ее частные производные по х ₁, х ₂ и λ приравняем их нулю. В результате получим систему уравнений

(23)

Из первого и второго уравнений имеем х _1- х ₂=0. Решая это уравнение совместно с третьим из системы (23), находим х ₁ = 5/2; x ₂=5/2. Таким образом, в точке (5/2; 5/2) данная функция может иметь условный экстремум. Чтобы определить, достигается ли в этой точке условный экстремум, нужно провести дополнительные исследования. В частности, используя вторые частные производные, можно показать, что в этой точке функция имеет условный минимум и F _min=25/2.

Метод множителей Лагранжа можно применять и в том случае, когда условия связи представляют собой неравенства. Так, если требуется найти экстремум функции z=f (X) при условии g (X)≤ b, то сначала следует найти точки безусловного экстремума функции z=f (X) из уравнений 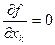(k =), затем среди этих точек отобрать те, координаты которых удовлетворяют условию связи g (X) <b, и, наконец, определить точки, удовлетворяющие системе уравнений

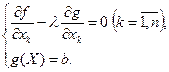
Точки, найденные в результате решения этой системы, вместе с точками, определенными на первом этапе и удовлетворяющими условию g (X)< b, подлежат дальнейшему исследованию, как и при нахождении безусловного экстремума.

Дата добавления: 2014-01-07