Выпуклое программирование

Математические основы выпуклого программирования.

Производная по направлению. Пусть дана функция z = f (x, у), определенная в замкнутой области D плоскости хОу (рис. 7.1). Известно, что частные производные 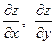функции z = f (x, у) могут быть истолкованы как скорости изменения этой функции в точке М ₀(х, у) в направлении осей Ох и Оy.

Рис. 71

Понятие производной можно обобщить, если рассматривать скорость изменения функции z=f(x, у) в произвольном направлении, образующем некоторый угол с осью Ох. Пусть 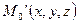— точка на поверхности z=f(x, у). Дадим аргументам х и у приращения . Тогда функция z получит приращение . Через обозначим точку на поверхности с координатами 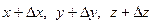; М₀(х,у) и М₁(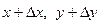) — проекции точек 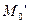и 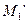на плоскость хОу. Обозначим через угол, который составляет прямая М₀М₁ с осью Ох (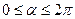), а через 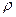— длину отрезка М₀М₁.

Определение 7.1. Производной 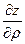функции z=f(x, у) в точке М₀(х,у) по направлению α называется предел отношения приращения 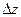функции z, возникшего при перемещении точки М из положения М₀ вдоль луча, состав­ляющего угол с положительным направлением оси Ох, к величине 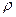этого перемещения, когда 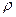стремится к нулю, т. е.

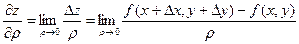(7.1)

Найдем формулу для вычисления производной по направлению в точке М (х, у) от функции z=f (x, у), дифференцируемой в этой точке. Из рис. 7 .1 видно, что .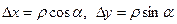

Используя эквивалентность полного приращения 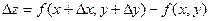и полного дифференциала 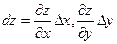, из формулы (7.1) получаем

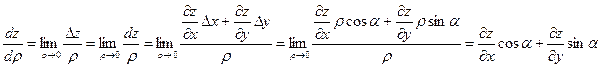поскольку значения производных 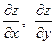и угол не зависят от 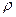. Итак,

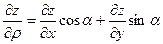(7.2.)

Таким образом, производная по направлению α является линейной комбинацией частных производных.

Если производная больше 0, то функция возрастает в указанном направлении, если меньше – убывает.

Градиент функции и его свойства. В математическом программировании наибольший интерес представляет вопрос о направлении наискорейшего возрастания функции в данной точке. Эта задача решается с помощью вектора, называемого градиентом функции.

Определение 7.2. Градиентом функции z=f(x, у) в данной точке М₀(х, у) называется вектор, расположенный в плоскости хОу, имеющий своими координатами частные производные функции z, вычисленные в этой точке.

Градиент обозначают grad f(x, у), .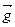

Итак, .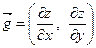

Теорема 7. 1. Направление градиента является направлением наискорейшего возрастания функции z=f(x, у); модуль градиента равен наибольшей скорости возрастания функции z.

Доказательство. На рис. 7.1 направление α дифференцирования определяется вектором 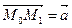. Единичный вектор 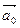этого направления имеет координаты cos α,sin α, поскольку .

Найдем скалярное произведение векторов 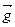и :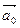

(,)=.

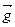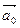Сравнивая это равенство с равенством (7.2), устанавливаем, что

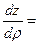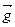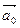(,) (7.3)

Обозначим угол между векторами 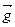,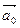через φ, получим

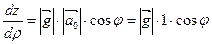
Если φ =0, т. е. если направление вектора 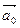(направление дифференцирования) совпадает с направлением градиента 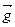, то cos φ достигает своего наибольшего значения (равного 1) и

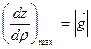(7.4)

Таким образом, производная функции z=f (x, у) достигает наибольшей величины по направлению градиента, что и свидетельствует о том, что в направлении градиента функция z возрастает с наибольшей скоростью. Из формулы (7.4) видно также, что наибольшая скорость возрастания функции z равна модулю градиента.

Что и требовалось доказать.

Пример 7.2. Найти направление наискорейшего возрастания функции z=x ₂ +ху+5 в точке M₀ (1;-1) и вычислить значение производной в этом направлении.

Решение. Находим координаты градиента дайной функции:

дz/дх=2х+у, дz/ду=х.

Итак, в точке М ₀ градиент имеет координаты 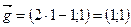. По координатам градиента видно, что искомое направление дифференцирования составляет угол 45° с осью Ох. Значение производной в этом направлении

.

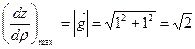Теорема 7.2. Градиент функции z=f(x, у) в каждой точке М₀(х; у) направлен по нормали к линии уровня поверхности z=f(x, у), проходящей через эту точку.

Доказательство. Пусть уравнение линии уровня l (рис. 7.2), проходящей через точку М₀, имеет вид

f(x,y)=C. (7.5)

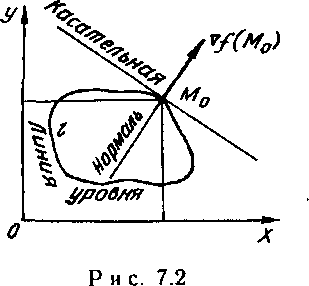
Чтобы найти угловой коэффициент k касательной в точке М ₀ к этой линии, продифференцируем равенство (7.5) как неявную функцию:

.

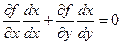Откуда

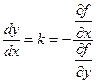. (7.6)

Найдем коэффициент 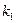прямой, на которой лежит градиент. Очевидно, что

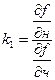(7.7)

Сравнивая равенства (7.6) и (7.7), видим, что kk ₁=-1, т. е. градиент и касательная взаимно перпендикулярны. Иначе говоря: градиент в данной точке направлен по нормали к линии уровня поверхности.

Что и требовалось доказать.

Обобщая понятие градиента на случай n -мерного пространства, примем следующее определение.

Определение 7.3. Если функция 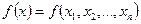дифференцируема в точке , то градиентом f (х) в точке х₀ называется n -мерный вектор, координаты которого равны частным производным функции f(x), вычисленным в точке х₀, т. е.

.

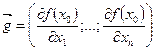Все свойства градиента, установленные в трехмерном пространстве, переносятся и в n-мерное пространство.

Вектор 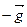противоположный градиенту, называется антиградиентом. Он указывает направление наискорейшего убывания функции f (x).

На замечательном свойстве градиента указывать в каждой точке, в которой он существует, направление наискорейшего возрастания функции, основаны градиентные методы решения задач математического программирования, в частности выпуклого программирования.

Выпуклые и вогнутые функции, их основные свойства. Важный класс задач математического программирования составляют задачи, модели которых содержат выпуклые (вогнутые) функции.

Определение 7.4. Функция f (x), определенная на выпуклом множестве X, называется выпуклой, если для любых точек х' и х" из этого множества и любого 0≤λ≤1 справедливо неравенство

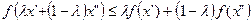. (7.8)

Если в соотношении (7.8) при 0< λ <1 и любых х ', х "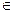 X (х '≠ x ") имеет место строгое неравенство, то f (x) называется строго выпуклой.

Определение 7.5. Функция f (x), определенная на выпуклом множестве X, называется вогнутой, если для любых точек х ' и х " из этого множества и любого 0≤ λ ≤1 справедливо неравенство

f (λ x '+(1- λ) x ")≥ λf (x ')+(1- λ) f (x "). (7.9)

Если в соотношении (7.9) при 0<λ<1 и любых х ', х "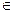 X (х '≠ x ") имеет место строгое неравенство, то f (x) называется строго вогнутой.

Геометрическая иллюстрация данных определений для двухмерного пространства ясна из рис. 7.3: выпуклая (рис. 7.3, а) функция f (x) на отрезке [ х '; х "] не может принимать больших значений, чем линейная функция, интерполирующая значения f (х ') и f (х "). В свою очередь вогнутая функция f (х) (рис. 7.3, б) не может принимать меньших значений, чем линейная функция, интерполирующая значения f (x ') и f (x ").

Рис. 7.3

Из определений 7.4 и 7.5 видно, что свойство выпуклости (вогнутости) функций предполагает выпуклость множества, на котором задана функция.

Можно доказать, что если функции f_i (x) 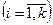являются выпуклыми на некотором выпуклом множестве X, то выпуклой на X будет и неотрицательная линейная комбинация этих функций, т. е. функция 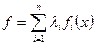при 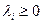, в частности выпуклой будет и сумма выпуклых функций.

Теорема 7.3. Если φ (х) — выпуклая функция при всех х ≥0, то будет выпуклым и множество решений системы φ (х) ≤b, х≥ 0.

Доказательство. Проверим, что вместе с решениями x ₁ и х ₂ системы φ (х) ≤b, х≥ 0, множеству решений этой системы принадлежит и любой вектор 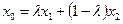, где 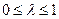. Ясно, что 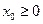. Остается показать, что φ (х ₀) ≤b. По свойству выпуклости функции 𝜑 (x)

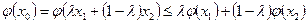(7.10)

Но 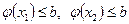, поэтому для любого 0≤ λ ≤1 справедливы неравенства 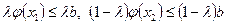. Складывая эти неравенства, получаем 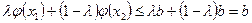. С учетом соотношения (7.10) приходим к неравенству φ (х ₀) ≤b.

Что и требовалось доказать.

Аналогичная теорема доказывается и для вогнутых функций.

Можно показать, что множество решений системы 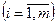выпукло, если в неравенствах со знаком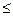 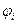- выпуклые функции, а в неравенствах со знаком 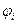— вогнутые функции для х ≥0.

Доказывается, что выпуклая функция f (x), определенная на выпуклом множестве X, непрерывна в любой внутренней точке этого множества.

Теорема 7.4. Если выпуклая функция f (x) дифференцируема во внутренних точках множества X, то для любых внутренних точек х ₁, и х ₂ имеет место неравенство

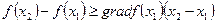(7.11)

Доказательство. Поскольку f (x) — выпуклая функция, то

,

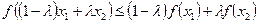Откуда

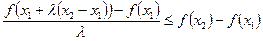(7.12)

Известно, что если функция f (x) одной переменной х в промежутке от x₀ до x₀+∆ x непрерывна и имеет непрерывную производную, то справедлива следующая формула Тейлора:

.

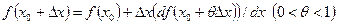В нашем случае речь идет о функции f (x), зависящей от n переменных, поэтому формула Тейлора в векторной записи принимает следующий вид:

.

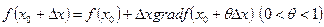Используя ее при х ₀= х ₁, ∆ x = λ (х₂- х ₁), будем иметь

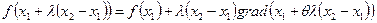(7.13)

Подставляя выражение (7.13) в неравенство (7.12), находим

.

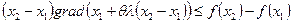Переходя к пределу при λ →0 в этом неравенстве, получаем соотношение (7.11).

Что и требовалось доказать.

Теорема 7.5. Выпуклая функция f (x), определенная на выпуклом множестве X, достигает своего глобального минимума в каждой точке х, в которой градиент функции обращается в нуль.

Доказательство. Пусть, например, в точке х ₀ градиент gradf (x ₀)=0. Покажем, что в этой точке функция f (х) имеет глобальный минимум, т. е. что для любой точки х 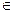Х справедливо неравенство f (x)≥f(x ₀). Известно, что для выпуклой на множестве X функции f (x) справедливо неравенство (7.11), где x ₁ и х ₂ — любые внутренние точки множества X. Полагая в неравенстве (7.11) х ₁= х ₀ и х ₂= х, получаем f (х)- f (х ₀)≥ gradf (x ₀)(х - х ₀), откуда f (x)≥ f (x ₀), что и доказывает теорему.

Что и требовалось доказать.

Теорема 7.6. Локальный минимум выпуклой функции f (x), определенной на выпуклом множестве X, совпадает с ее глобальным минимумом на этом множестве.

Доказательство. Пусть функция f (х) в точке х ₀ имеет локальный минимум, т. е. для всех точек х из некоторой ε -окрестности точки х ₀ справедливо неравенство

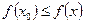(7.14)

Докажем, что неравенство (7.14) справедливо для любой точки допустимой области X. Предположим противное, т. е. что в области X существует точка х ' такая, что

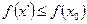(7.14)

и, следовательно, х₀ не является точкой глобального минимума.

Рассмотрим отрезок, соединяющий точки х ' и х ₀. Его уравнение имеет вид 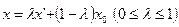. Ввиду того, что допустимая область X выпуклая, отрезок х ' х ₀ полностью лежит в ней. Возьмем на нем точку х ", лежащую в ε -окрестности точки х ₀, но не совпадающую с точкой х ₀. Поскольку точка х " расположена на отрезке х'х ₀, ей отвечает некоторая определенная величина λ=λ" и выполняется условие х"=λ"х'+(1- λ" )х ₀ (0<λ"<1). В силу выпуклости функции f(х) для точек х' и х₀ имеет место неравенство 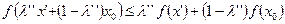или

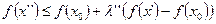(7.16)

Но по предположению выполняется неравенство (7.15), а поэтому в соотношении (7.16) 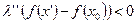. Отбрасывая это слагаемое, мы можем только усилить неравенство (7.16), т. е. получаем

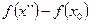(7.17)

Однако неравенство (7.17) противоречит условию (7.14) для точек ε-oкрестности точки х ₀. Значит, в допустимой области X нет точек типа х ', для которых выполняется условие (7.15). Следовательно, точка х ₀ действительно является точкой глобального минимума.

Что и требовалось доказать.

Для практической проверки функции на выпуклость может оказаться полезным следующее свойство выпуклых функций: функция f(х) будет выпуклой, если ее вторые частные производные образуют матрицу, в которой все главные миноры неотрицательны.

7.2. Задача выпуклого программирования.

Задача математического программирования

max (min) z=f (x); (7.18)

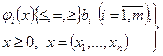(7.19)

в которой либо целевая функция (7.18), либо ограничения (7.19), либо и то и другое нелинейны, называется нелинейной.

Нелинейные задачи составляют широкий класс настолько сложных задач, что до сих пор невозможно разработать общие методы, подобные симплекс-методу в линейном программировании, которые позволяли бы решать любые нелинейные задачи. Но, несмотря на отсутствие универсальных методов, разработаны способы решения отдельных специальных классов задач, и прежде всего задач с выпуклыми (вогнутыми) функциями f (х) и φ_i(x).

В теории выпуклого программирования в качестве основной обычно рассматривается задача минимизации выпуклой функции п переменных z=f (x) при ограничениях 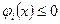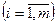, , 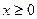где функции 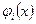предполагаются выпуклыми. Выпуклость множества допустимых решений задачи следует из теоремы 7.3.

Если f(x) и 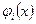являются вогнутыми функциями, то имеем задачу максимизации f(x) при ограничениях , .

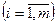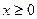Дата добавления: 2014-01-07