Оптимальное планирование производства при ограниченных запасах ресурсов

Постановка задачи. Имеются n видов продукции и m видов ресурсов в количествах b₁, b₂ ,…b_m для их производства. Задана матрица А= || a_ij ||, , , где a_ij характеризует нормы расхода i-го ресурса на изготовление единицы продукции j-го вида. От реализации единицы каждого вида продукции предприятие получает прибыль с_j, удовлетворяющую условию линейности. Требуется определить такой план выпуска продукции (оптимальный ассортимент), при котором суммарная прибыль была бы максимальной.

План выпуска продукции - это количество единиц каждого вида продукции, которое надо выпустить. Обозначим план выпуска продукции через х =(х₁,х₂, …,х_n), где х_j 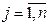- количество единиц j-го вида продукции.

Математическая модель этой задачи имеет вид:

max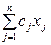

при ограничениях

,

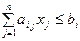(i – индекс вида ресурсов от i=1 до i=m;

j – индекс вида продукции от j=1 до j =n;

a_ij – норма расхода ресурсов i -го вида на единицу продукции j-го типа;

c_j – прибыль от реализации единицы продукции j-го типа).

Ограничения записаны с учетом того, что затраты ресурсов на производство продукции не должны превышать имеющихся запасов ресурсов. Условие неотрицательности означает, что план выпуска продукции не может быть отрицательной величиной. Кроме ограничений на ресурсы в эту модель можно ввести дополнительные ограничения на планируемый выпуск продукции, то ест ь .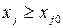

Все данные задачи можно свести в таблицу.

Виды продукции Виды ресурсов	А1	А2	…	Аn	Запасы ресурсов
Нормы расходов ресурсов
Ресурс1	a11	a12	…	a1n	b1
Ресурс1	a21	a21	…	a2n	b2
…	…	…	…	…
Ресурс1	am1	am2	…	amn	bm
Прибыль от реализации единицы продукции	с1	с2	…	cn

Пример1.

Цех химического завода выпускает два вида продукции А₁ и А₂. Известны нормы расхода ресурсов (рабочего времени, оборудования, сырья), суточный объемы ресурсов цеха («запасы») и прибыль от реализации каждого продукции. Требуется составить такой суточный план выпуска, чтобы прибыль от её реализации была максимальной.

Виды ресурсов	Нормы расходов ресурсов	Суточный объем ресурсов
А1	А2
Сырье, кг	3	6	17
Рабочее время, час	8	4	23
Оборудование, кол-во	4	3	11
Прибыль	3	2

Математическая модель ЗЛП:

f(x)=(3x₁ + 2x₂)→ max

при ограничениях

3x₁ + 6x₂ ≤ 17

8x₁ + 4x₂ ≤ 23

4x₁ + 3x₂ ≤ 11

х₁ ≥ 0, х₂ ≥ 0

Дата добавления: 2014-01-07