Испытание, эксплуатация и ремонт

Задача о смесях

Постановка задачи. Имеются n компонентов, при сочетании которых в разных пропорциях получают разные смеси. Каждый компонент, а следовательно и смесь, содержит m веществ. Количество i-го вещества, входящего в состав j-го компонента и в состав единицы смеси, обозначим через a_ij и a_i соответственно, 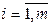, 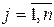. Пусть a_i линейно зависит от a_ij, то есть

a_i = ,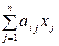

где х_j – доля (процентное содержание) j-го компонента в составе смеси. Заданы величины с_j, 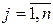, характеризующие калорийность (стоимость, массу) единицы j-го компонента и величины b_i, 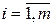, указывающие минимально необходимое процентное содержание i-го вещества в смеси. Требуется определить оптимальный состав смеси, то есть долю х_j j-го компонента в составе смеси.

Математическая модель этой задачи имеет вид:

max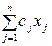

при ограничениях

,

Первое ограничение означает, что процентное содержание i-го вещества в единице смеси должно быть не менее b_i. Второе ограничение показывает, что доли всех компонентов в сумме равны 1.

Пример2. Стандартом требуется, чтобы октановое число бензина А-76 было не ниже 76%, а содержание серы – не более 0,3%. Для изготовления бензина используется смесь из четырех компонентов. Известны октановые числа компонентов, содержание в них серы, запасы компонентов.

Компоненты	%содержания	Запасы компонентов, т	Стоимость компонента
Октановое число	Сера
	68	0,35	700	40
	72	0,35	600	45
	80	0,30	500	60
	90	0,20	300	90

Требуется определить, какое количество каждого компонента следует использовать для получения 1000 т автомобильного бензина А-76, чтобы его стоимость была минимальной.

Решение.

Обозначим через х_j, j=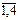, объем производства j-го компонента. Математическая модель этой ЗЛП:

f(x)=(40x₁ + 45x₂ + 60x₃ +90x₄)→ min

при ограничениях

по количеству бензина: x₁ + x₂ + x₃ + x₄ =1000

по октановому числу: 68x₁ + 72x₂ + 80x₃ +90x₄ ≥ 76·1000

по содержанию серы: 0,35 x₁ + 0,35x₂ + 0,3x₃ + 0,2x₄ ≤ 0,3·1000

по запасам компонентов: 0 ≤ х₁ ≤ 700,

0 ≤ х₂ ≤ 600,

0 ≤ х₃ ≤50 0,

0 ≤ х₄ ≤ 300.

судовых электротехнических устройств

Дата добавления: 2014-01-07