
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Эффективная плотность состояний в валентной зоне
|
|
|
|
Для того чтобы рассчитать равновесные концентрации электронов n0 и дырок p0 необходимо рассчитать значения интеграла Ферми-Дирака (2.52) и (2.56), что представляет значительные трудности для всего диапазона положения уровня Ферми в зонах η. Аналитические решения для интеграла Ферми-Дирака существуют только для крайних случаев – невырожденного и сильно-вырожденного полупроводника.
Рассмотрим три случая.
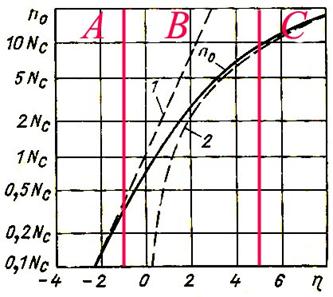
Первый соответствует невырожденному примесному полупроводнику (рис. 2.7, область A, рис. 2.8).
Принято считать, что полупроводник не вырожден, если:
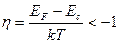 или
или 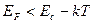 (2.57)
(2.57)
Это означает, что в невырожденном донорном полупроводнике уровень Ферми лежит ниже дна зоны проводимости по крайней мере на несколько кТ. В этом случае для электронов, находящихся в зоне проводимости и обладающих энергией  , в функции распределения Ферми-Дирака экспоненциальный член будет намного больше единицы, поэтому
, в функции распределения Ферми-Дирака экспоненциальный член будет намного больше единицы, поэтому
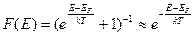 (2.58)
(2.58)
Таким образом, в невырожденном полупроводнике носители заряда подчиняются статистике Больцмана. В соответствии с этим интеграл Ферми запишется в виде:
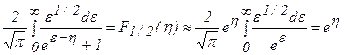 (2.59)
(2.59)
Равновесные концентрации электронов n0 и дырок p0 для случая невырожденного полупроводника соответственно равны (рис. 2.7 (А), рис. 2.8):
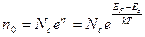 (2.60)
(2.60)
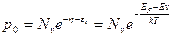 (2.61)
(2.61)
Физический смысл параметров Nc и Nv – плотность состояний в зоне проводимости и валентной зоне. Формулы для Nc и Nv определяют пределы заполнения энергетических уровней вблизи дна зоны проводимости и валентной зоны.
Зная концентрацию свободных носителей заряда можно оценить положение уровня Ферми в запрещенной зоне. Для полупроводника n-типа проводимости при комнатной температуре эту зависимость можно записать в виде:
 (2.61а)
(2.61а)
| ||
 или или 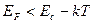
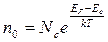
| -1<η<5
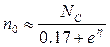
| 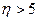 или или 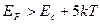
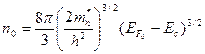
|
| Рис. 2.7. Зависимость концентрации электронов проводимости n0 от положения приведенного уровня Ферми. | ||
| ||
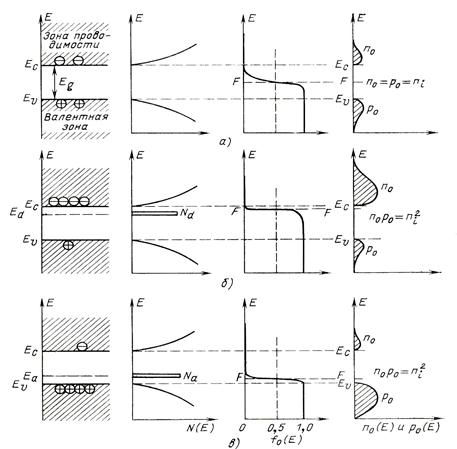
| Рис. 2.8. Зонная диаграмма, плотность состояний, распределение Ферми-Дирака и концентрация носителей заряда в собственном (а), донорном (б) и акцепторном (в) полупроводниках при термодинамическом равновесии. |
Если уровень Ферми совпадает с дном зоны проводимости (т.е. EF = EC), тогда из формулы 2.60 следует, что no=NC. Т.е. при легировании полупроводника донорной примесью до концентрации no ~ NC - уровень Ферми приближается к краю запрещенной зоны (аналогично – для легирования акцепторной примесью). Полупроводник является вырожденным, если уровень Ферми расположен вблизи границ разрешенной зоны (в интервале ± несколько kT от EC или EV).
В Si при Т=300 К: Nc =2.8*1019cm-3 Nv =1019cm-3
Второй случай - сильно вырожденный примесный полупроводник(рис. 2.7, область C, рис.2.9.
Донорный полупроводник считается сильно вырожденным при:
 (2.62)
(2.62)
т.е. когда уровень Ферми расположен в зоне проводимости по крайней мере на 5 кТ выше Еc. Условие (2.62) действует и при очень низкой температуре. Если kT à 0, то η0 à ∞ (здесь η0 – приведенный уровень Ферми при нулевой температуре). В этом случае в выражении (2.52) знаменатель = 1, а бесконечный верхний предел интегрирования можно заменить η0. Тогда равновесная концентрация электронов в сильно вырожденном донорном полупроводнике будет равна:
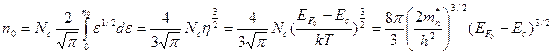 (2.63)
(2.63)
При этом концентрация дырок в сильно-вырожденном полупроводнике n -типа проводимости задается формулой (2.61)!!!
Зная концентрацию свободных носителей заряда можно определить положение уровня Ферми:
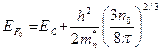 (2.63а)
(2.63а)
Равновесная концентрация дырок в сильно вырожденном акцепторном полупроводнике запишется следующим образом:
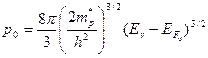 , (2.64)
, (2.64)
При этом концентрация электронов находится из соотношения (2.60).
Из равенств (2.63) и (2.64) следует, что концентрация свободных носителей заряда в сильно вырожденном полупроводнике не зависит от температуры. Она определяется положением уровня Ферми и величиной эффективной массы. При этом, чем меньше эффективная масса носителей заряда, тем соответственно и меньше их концентрация, при которой наступает вырождение.
 E
EF
EC
ED Eg
EV E
EF
EC
ED Eg
EV
|  E
N(E)
N(E) E
N(E)
N(E)
|  E
EF
EC
EV
F(E) E
EF
EC
EV
F(E)
|  E
EF
EC
EV
n0; p0 E
EF
EC
EV
n0; p0
|
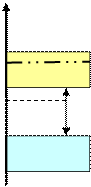
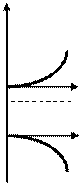
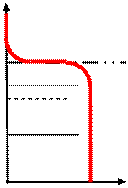
Рис. 2.9. Зонная диаграмма, плотность состояний, распределение Ферми-Дирака и концентрация носителей заряда в сильно-вырожденном полупроводнике n- типа проводимости при термодинамическом равновесии.
Третий случай – вырожденный полупроводник (рис. 2.7, область В).
При расположении уровня Ферми вблизи границы зон (зона проводимости/запрещенная зона) -1<η<5, точного (аналитического) выражения для интеграла Ферми-Дирака не существует. В этом случае используют либо табулированные (численно-рассчитанные) значения интеграла Ферми-Дирака, либо применяют полуэмпирические формулы, например, в виде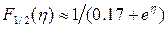 . Тогда зависимость n0 в зоне проводимости от положения уровня Ферми может быть представлена как:
. Тогда зависимость n0 в зоне проводимости от положения уровня Ферми может быть представлена как:
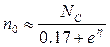 (2.65)
(2.65)
Вместе с тем, расчет концентрации носителей по формуле (2.65) может давать существенную погрешность, поэтому на практике, как правило, используют специальные таблицы интегралов Ферми-Дирака. Зависимость интеграла Ферми-Дирака F1/2 от η при расположении уровня Ферми вблизи зоны проводимости в интервале EC ± 6 kT представлена на рис. 2.6.
|
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 10938; Нарушение авторских прав?; Мы поможем в написании вашей работы!