Теорема Остроградского-Гаусса

Рассмотрим некоторую произвольную замкнутую поверхность S. Если разбить эту поверхность на малые площадки D S_i, определить элементарные потоки DF _i поля E через эти малые площадки, а затем их просуммировать, то в результате мы получим поток F вектора E через замкнутую поверхность S (рис. 1.5.1):

. (1.5.1)

В случае замкнутой поверхности всегда выбирается внешняя нормаль.

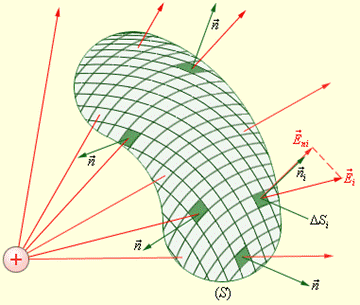
Рис. 1.5.1. Рис. 1.5.2.

Теорема Остроградского-Гаусса. Поток вектора напряженности электростатического поля через произвольную замкнутую поверхность пропорционален полному заряду, заключенному внутри этой поверхности. Коэффициент пропорциональности равен 4 pk, где k – коэффициент пропорциональности в законе Кулона.

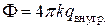. (1.5.2)

В СИ эта формула имеет вид:

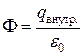. (1.5.3)

Доказательство.

1. Рассмотрим сначала сферическую поверхность S₀ радиуса r, в центре которой находится точечный заряд q (рис. 1.5.2). Электрическое поле в любой точке сферы перпендикулярно к ее поверхности и равно по модулю

. (1.5.4)

Тогда поток F₀ через сферическую поверхность S₀ равен 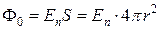, Þ .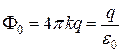

2. Докажем теорему Гаусса для случая точечного заряда q, расположенного внутри произвольной замкнутой поверхностью S (рис. 1.5.3). Будем называть такую поверхность гауссовой поверхностью. Проведем внутри этой поверхности вспомогательную сферу S ₀ радиуса R ₀, в центре которой находится заряд q.

Рис. 1.5.3.

Рассмотрим конус с малым телесным углом ΔΩ при вершине. Этот конус выделит на сфере малую площадку Δ S ₀, а на поверхности S – площадку ΔS. Элементарный поток ΔF₀ через площадку Δ S ₀ равен

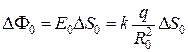, (1.5.5)

а через площадку Δ S -

, (1.5.6)

где 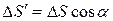– площадь площадки, выделяемой конусом с телесным углом ΔΩ на поверхности S на расстоянии r от точечного заряда q.

Обозначим D ₀ и D ¢ - диаметры площадок Δ S ₀ и Δ S ¢. Из подобия соответствующих треугольников следует

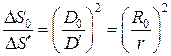. (1.5.7)

Сравнивая выражения (1.5.5) и (1.5.6), и учитывая (1.5.7), получим, что

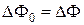. (1.5.8)

Откуда следует, что полный поток F электрического поля точечного заряда q через произвольную поверхность, охватывающую заряд, равен потоку F₀ через поверхность вспомогательной сферы:

. (1.5.9)

3. Аналогичным образом можно показать, что, если замкнутая поверхность S не охватывает точечного заряда q, то поток F = 0. Такой случай изображен на рис. 1.5.1. Все силовые линии электрического поля точечного заряда пронизывают замкнутую поверхность S насквозь. Внутри поверхности S зарядов нет, поэтому в этой области силовые линии не обрываются и не зарождаются.

4. Обобщим теорему Гаусса на случай произвольного заряженного тела или системы точечных зарядов. Такую систему можно представить как систему точечных зарядов q_i (i = 1, …, n).

Из принципа суперпозиции следует, что поле любого распределения зарядов можно представить как векторную сумму электрических полей точечных зарядов. Тогда поток F системы зарядов через произвольную замкнутую поверхность S будет складываться из потоков F _i электрических полей отдельных зарядов. Если заряд q_i оказался внутри поверхности S, то он дает вклад в поток, равный 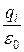; если же этот заряд оказался снаружи поверхности, то вклад его электрического поля в поток будет равен нулю.

Таким образом, теорема Гаусса доказана.

Замечание. Для доказательства теоремы Гаусса существенны два свойства электрического поля:

1. зависимость кулоновской силы взаимодействия двух точечных зарядов как ;

2. принцип суперпозиции полей.

Для всех взаимодействий, удовлетворяющих обоим перечисленным свойствам, выполняется теорема Гаусса. В частности, она справедлива для гравитационного поля.

Дата добавления: 2014-01-07