Применение теоремы Остроградского-Гаусса

I. Электрическое поле равномерно заряженного шара.

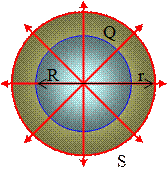
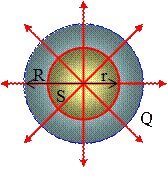
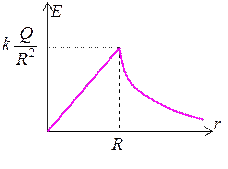
Рис. 1.6.1. Рис. 1.6.2. Рис. 1.6.3.

Пусть Q – заряд шара (для удобства, будем считать Q > 0), R – его радиус. Очевидно, силовые линии электрического поля шара имеют радиальную симметрию. Найдем зависимость напряженности электрического поля шара от расстояния r от центра шара. Для этого в качестве гауссовой поверхности S выберем сферу радиуса r.

В случае r ³ R (рис. 1.6.1) из теоремы Гаусса следует, что поток F вектора напряженности через гауссову поверхность S равен

, Þ

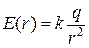, . (1.6.1)

Таким образом, поле заряженного шара (или сферы) ведет себя на расстояниях больших радиуса шара (сферы) подобно полю точечного заряда.

В случае r £ R (рис. 1.6.2) поток F вектора напряженности через гауссову поверхность S представляется в виде:

,

где Q_внутр. – часть заряда равномерно заряженного шара, лежащего внутри гауссовой поверхности S.

Если ввести объёмную плотность заряда, т.е. заряд единицы объёма,

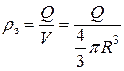, (1.6.2)

то 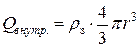, Þ

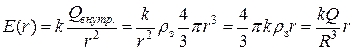. (1.6.3)

График зависимости E(r) для равномерно заряженного шара приведен на рис. 1.6.3.

II. Электрическое поле бесконечной равномерно заряженной плоскости.

Найдем напряженность E (r) электрического поля на расстоянии r от плоскости. В силу симметрии поле равномерно заряженной плоскости должно быть везде направлено по нормали.

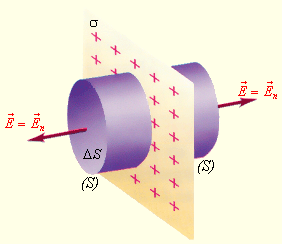
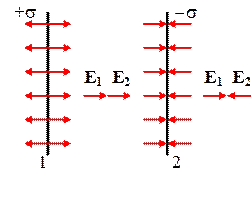
Рис. 1.6.4. Рис. 1.6.5.

В этом случае гауссову поверхность S целесообразно выбрать в виде цилиндра длины 2 r и площадью основания Δ S (рис. 1.6.4). Ось цилиндра направлена перпендикулярно заряженной плоскости, а его основания расположены на одинаковом расстоянии r от нее.

Поток вектора напряженности через выбранную поверхность равен

. (1.6.4)

Поток через боковую поверхность равен 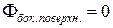, т.к. нормаль к боковой поверхности перпендикулярна вектору напряженности. Поток через оба основания равен .

Обозначим 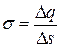поверхностную плотность заряда, т.е. заряд единицы площади. В случае равномерно заряженной плоскости .

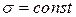Внутри гауссовой поверхности находится заряд 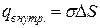. Применение теоремы Гаусса дает:

, Þ 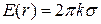, (1.6.5)

или в системе СИ

. (1.6.6)

Выражения (1.6.5) и (1.6.6) показывают, что напряженность электрического поля бесконечной равномерно заряженной плоскости не зависит от расстояния r. Таким образом, поле бесконечной равномерно заряженной плоскости – однородное.

Полученное выражение для электрического поля однородно заряженной плоскости применимо и в случае плоских заряженных площадок конечного размера. В этом случае расстояние от точки, в которой определяется напряженность поля, до заряженной площадки должно быть значительно меньше размеров площадки.

Теперь рассмотрим поле, создаваемое двумя параллельными бесконечно заряженными плоскостями, имеющими одинаковые заряды противоположных знаков. Такая система называется плоским конденсатором (рис. 1.6.5).

Напряженность поля вне конденсатора равна

, (1.6.7)

т.к. ; а внутри конденсатора

. (1.6.8)

III. Электрическое поле бесконечной равномерно заряженной нити.

Найдем напряженность E (r) электрического поля на расстоянии r от равномерно заряженной нити. В силу симметрии линии напряженности перпендикулярны поверхности нити. Выберем в качестве гауссовой поверхности S цилиндр высотой l, в основании которого круг радиуса r (рис. 1.6.6). Ось цилиндра совпадает с заряженной нитью.

Поток вектора напряженности через гауссову поверхность равен

. (1.6.9)

Т.к. силовые линии электрического поля параллельны основаниям цилиндра, то поток через основания равен 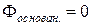. Поток через поверхность S равен потоку через боковую поверхность.

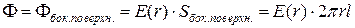. (1.6.10)

Введем линейную плотность заряда: 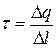, которая равна заряду единицы длины нити. В случае равномерно заряженной нити .

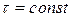Тогда из теоремы Гаусса следует

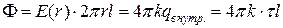, Þ

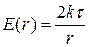, (1.6.11)

или в системе СИ

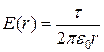. (1.6.11)

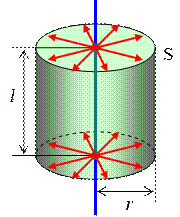
Рис. 1.6.6.

Дата добавления: 2014-01-07