Область их сходимости

Функциональные ряды: Область сходимости, правильно сходящиеся ряды, их свойства. Степенные ряды.

Лекция № 3

Рассмотрим ряды, членами которого являются не числа, а некоторые функции:

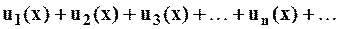(1)

¨ Ряды вида (1) называются функциональными. Полагаем, что все функции 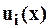– определены и непрерывны в одном и том же интервале (конечном или бесконечном).

Ряд (1) может для одних значений “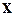” сходится, для других – расходится.

¨ Значение 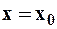, при котором числовой ряд сходится, называется точкой сходимости функционального ряда (1).

¨ Совокупность значений “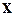”, при которых ряд (1) сходится называется областью сходимости функционального ряда (1).

Пример 1. Рассмотрим ряд: Если 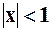, то данный ряд–это бесконечно убывающая геометрическая прогрессия, и она имеет сумму, равную , где . Для значений данный ряд расходится. Отсюда следует, что областью сходимости данного ряда является интервал: .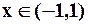

Сумма функционального ряда также является некоторой функцией, зависящей от “”: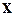

.

Так в примере 1: , причём эта сумма имеет смысл только при 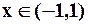, т.е. в области сходимости данного функционального ряда.

По аналогии числовых рядов введём понятие “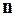”–ной частичной суммы ряда (1) и “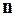”– го остатка ряда соответственно:

, .

Если для какого–то (из области сходимости ряда) ряд сходится, то верны равенства: и .

Известно, что сумма конечного числа слагаемых, каждое из которых есть непрерывная функция, есть функция непрерывная. Производная и интеграл от суммы конечного числа непрерывных функций также равна соответствующей сумме производных и интегралов от этих функций. Можно ли переносить указанные свойства на бесконечное число слагаемых? Можно, но не всегда!

Пример 2. Рассмотрим ряд: .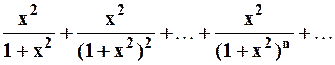

Если , то 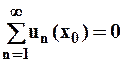. Если , то ряд – убывающая геометрическая прогрессия, и тогда:

.

Таким образом . Т.е. функция 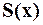– разрывная функция, хотя функции 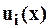– функции непрерывные.

¨ Функциональный ряд (1) называется правильно сходящимся (или мажорируемым) в области D, принадлежащей области сходимости ряда, если :

, где ряд – сходящийся ряд.

Пример 3. Рассмотрим ряд: 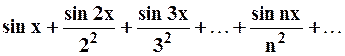. Этот ряд правильно сходится 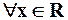, так как , а ряд – сходится.

Дата добавления: 2014-01-07