Степенные ряды. Интервал и область сходимости

¨ Степенным рядом называется функциональный ряд:

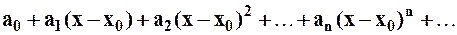, (1)

где 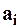– называются коэффициентами степенного ряда. Если 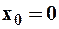, то получим ряд по степеням “”:

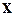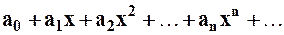, (2)

где 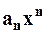– “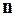” – ный член ряда, 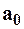– нулевой член ряда.

Теорема 1: (Абеля) Если степенной ряд (2) сходится в 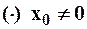, то он сходится и притом абсолютно в интервале: 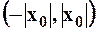, т.е. .

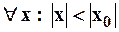Доказательство:

Пусть степенной ряд (2) сходится в 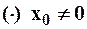, т.е. ряд 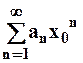– сходится тогда 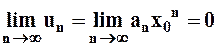, тогда 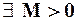такое, что 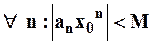. Перепишем ряд (2) в виде: 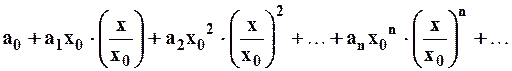и составим ряд, полученный из абсолютных величин членов исходного ряда:

,

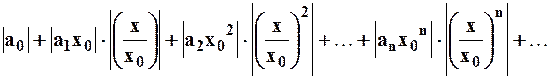причём: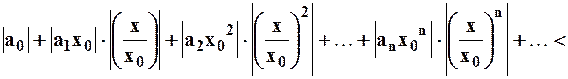

.

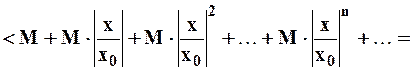
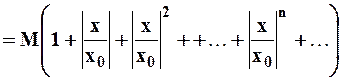В скобках стоит бесконечно убывающая геометрическая прогрессия, ес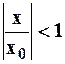ли или 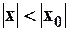. Таким образом исходный ряд ограничен сверху абсолютно сходящимся рядом. Значит исходный ряд также сходится абсолютно при .

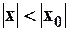Следствие: Если степенной ряд (2) расходится в 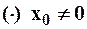, то он расходится и при всяком .

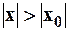Действительно, пусть 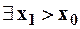при котором он сходится, тогда по теореме Абеля 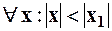ряд должен сходится, в том числе и в 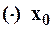, что противоречит условию.

Теорема Абеля позволяет определить интервал сходимости степенного ряда.

Вся числовая ось может быть представлена в виде множества точек, где степенной ряд либо сходится, либо расходится (в окрестности 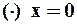для ряда (2) или 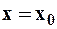для ряда (1)). Причём если границей интервала сходимости является 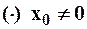, то при 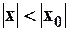ряд сходится, а при 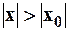ряд расходится. В граничных же точках ряд может либо сходиться, либо расходиться.

¨ Радиусом сходимости степенного ряда (2) называется такое число 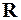, что для всех 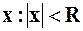– степенной ряд сходится, а для всех 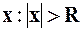ряд расходится.

¨ Интервал 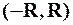называется интервалом сходимости степенного ряда (2). Принимаем, что для рядов, расходящихся при всех действительных чисел, кроме 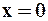, радиус сходимости 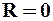, а для рядов, сходящихся для всех действительных чисел .

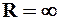Для степенных рядов (1) всё сказанное остаётся в силе; центр интервала сходимости будет находиться в 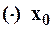, т.е. интервал 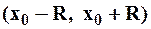является интервалом сходимости ряда.

Рассмотрим ряд, составленный из абсолютных величин членов ряда (2):

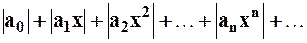. Данный ряд будет сходиться (т.к. он знакоположительный и к нему применим, например, признак Даламбера) если 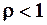и расходиться, если 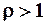, где 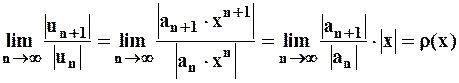. Множество значений 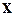, при которых данный предел меньше 1 и будет интервалом сходимости степенного ряда.

Пример 5. Рассмотрим степенной ряд:

.

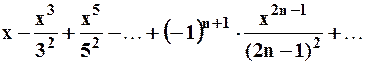Здесь: 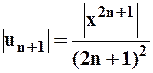, 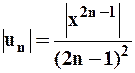. Рассмотрим: .

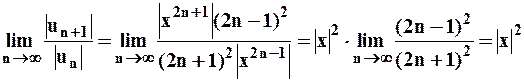На основании признака Даламбера, получим: при 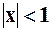– ряд будет сходиться, а при 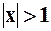– ряд будет расходиться. Для установления области сходимости рассмотрим поведение ряда в граничных точках:

Пусть 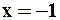: тогда ряд будет числовым
.

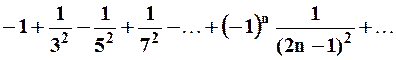При 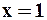имеем: 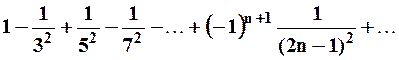. Наряду с полученными знакочередующимися числовыми рядами рассмотрим ряд:

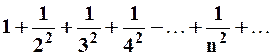– этот ряд сходящийся и ограничивающий сверху имеющиеся ряды. Последний ряд сходится. Отсюда следует, что ряды в граничных точках интервала также сходятся. Тогда областью сходимости исходного ряда будет область: .

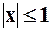Пример 6. Найдём область сходимости ряда:

.

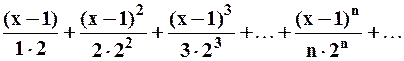Составим отношение: .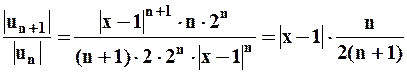

Найдём .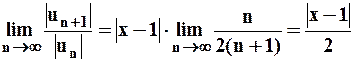

Согласно признаку Даламбера, ряд будет сходиться, если 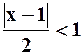, т.е. 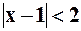. Таким образом, интервалом сходимости ряда является интервал: 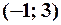. Для определения области сходимости ряда рассмотрим поведение ряда в граничных точках интервала:

Пусть :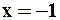

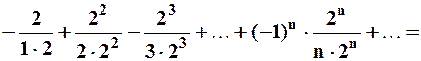
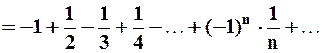– ряд Лейбница, он сходится.

Рассмотрим вторую границу:

:

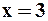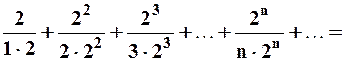
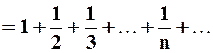– гармонический ряд, он расходится. Таким образом, областью сходимости данного ряда является множество .

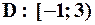Дата добавления: 2014-01-07