Операторный метод расчета переходных процессов

Управление потоком

Замечания о комментариях

После нахождения нужной информации можно скопировать ее в буфер обмена, затем переключиться в окно программного кода и вставить содержимое буфера обмена в свою программу. Такой метод гарантирует отсутствие синтаксических ошибок.

Комментарии компилятором VB игнорируются, они не увеличивают объём компилированной программы, а хранятся только в текстовом файле проекта. Таким образом, они не замедляют выполнение программы, но использование их очень полезно.

Комментарий начинается с апострофа как в начале строки, но может быть добавлен и в конец строки с активным программным кодом. Единственно, когда нельзя разместить комментарий в конце строки, это тогда, когда используется символ переноса строки. В этом случае комментарий размещается в отдельной строке.

Комментарии нужно использовать всегда! Потому что логика рассуждений забывается, и они могут избавить вас от очень трудной работы по восстановлению понимания цели программы.

Комментарии можно использовать и для удаления из потока выполнения программы ненужных операторов. Это особенно необходимо, когда нужно сравнить эффективность работы нескольких альтернативных решений или для того, чтобы временно исключить фрагмент кода, содержащий ошибку, пока отлаживается другая часть программы.

Управляющие структуры можно разбить на 3 главные группы:

- операторы условного и безусловного перехода;

- циклы;

- операторы With.

Оператор условного перехода определяет, какую из ветвей кода выполнять в зависимости от того, какое значение (True или False).

Цикл повторяет выполнение некоторого блока кода либо заданное число раз, либо пока некоторое условие не примет значение True или False.

Оператор With позволяет выполнить множество действий с одним и тем же объектом без необходимости каждый раз указывать имя объекта.

Использование логических операций в условиях:

And – только если оба выражения принимают значение True;

Or – если хотя бы одно из двух выражений True;

Xor – если только одно из выражений True.

Смысл операторного метода расчета – переход от дифференциальных уравнений к линейным. Если функция удовлетворяет условию Дирихле: является непрерывной или имеет на конечном интервале времени конечное число разрывов первого рода и конечное число максимумов и минимумов, и

,

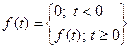то данная функция представима в виде:

, где - оператор Лапласа.

Интеграл имеет конечное значение в том случае, если растет не быстрее, чем :

,

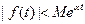где и - конечные вещественные числа, причем . Подобное преобразование функции получило название преобразование Лапласа.

Следующий интеграл представляет собой обратное преобразование Лапласа – переход из области изображений в область оригиналов:

Размерность переменной (т.е. тока или напряжения) в области изображений равна размерности оригинала, умноженной на секунду. Существует т.н. преобразование Карссона, для которого размерность изображения совпадает с размерностью оригинала:

.

Итак, с помощью преобразования Лапласа определим изображение функции :

,

где L – оператор Лапласа. Рассмотрим свойства функций и :

1. Если , то

.

1. Если и , то

.

1. Пусть , тогда

,

где - затухающая функция при , а - единичный вектор, т.е. получаем произведение затухающей функции на ограниченную, которое в пределе дает 0, поэтому

.

1. Пусть , найдем изображение функции :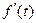

Снова возникает неопределенность в верхней подстановке, т.е. при . Для того, чтобы интеграл имел конечное значение, должно расти не быстрее чем (см. начало лекции). Поэтому затухает быстрее, чем растет . Поэтому произведение этих функций при стремится к нулю, а значит

,

таким образом,

.

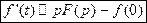В общем случае для производной n -го порядка при ненулевых начальных условиях имеем:

.

При нулевых начальных условиях имеем:

.

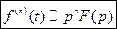1. Пусть , найдем изображение функции :

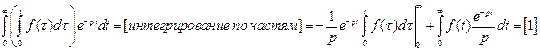
Нижняя подстановка в первом слагаемом, очевидно, = 0. Поскольку функция растет не быстрее, чем , интеграл тем более будет расти не быстрее, тогда и верхняя подстановка в первом слагаемом в пределе обращается в ноль, тогда

, т.е.

,

причем это выражение справедливо как при нулевых, так и при ненулевых начальных условиях.

!ВАЖНО! В общем случае преобразование Лапласа для ненулевых начальных условий отличается от преобразования для нулевых начальных условий (см. свойство 4).

Рассмотрим конкретные примеры: найдем изображения по Лапласу токов и напряжений на реактивных элементах. Пусть 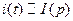, найдем изображение функции :

.

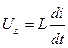
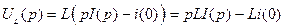Теперь найдем изображение функции :

.

Не забываем о том, что изображением константы по Лапласу является эта константа, умноженная на р, тогда

,

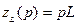
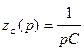эти значения получили название операторные сопротивления индуктивности и емкости соответственно.

1. Пусть 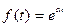, найдем изображение этой функции;

,

верхний предел обращается в ноль из тех же соображений, что и в предыдущих случаях.

1. Пусть , найдем изображение этой функции, сведя этот случай к предыдущему. Интеграл брать непосредственно мы не будем, а воспользуемся выражением комплексного синуса через экспоненты:

.

Аналогичное выражение можно получить для :

.

Дата добавления: 2014-01-07