Принцип последовательной проводки заявок

Принцип состоит в том, что каждая заявка отслеживается от момента поступления ее в систему до момента ее выхода из системы. И только потом рассматривается следующая заявка.

Рассмотрим работу алгоритма на примере двухканальной системы массового обслуживания заявок с двумя местами в общей очереди с дисциплиной FIFO и отказами при переполнении очереди (см. рис. 32.4), см. также лекцию 30.

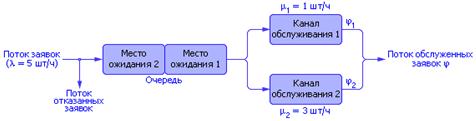
Рис. 32.4. Схема системы массового обслуживания

с двумя каналами и ограниченной очередью

Обозначим: λ — интенсивность прихода заявки; μ_i — интенсивность обслуживания заявки.

Построим алгоритм, определяющий вероятности обслуживания заявок и отказа заявок, а также пропускную способность системы.

Чтобы понять работу алгоритма, представьте себе для наглядности параллельные линейки — оси времени для каждого из мест, в которых может оказаться заявка в процессе обслуживания — так, как мы это делали ранее (см. лекцию 30).

Генерируем заявку (блоки 3, 4 — здесь и далее см. блоки на рис. 32.6). Случайный момент времени, когда заявка пришла в систему, равен T_с. Время между двумя случайными заявками имитируется формулой τ:= –1/λ · Ln(r), которое прибавляется к T_с предыдущей заявки T_с:= T_с – 1/λ · Ln(r). Учтем этот факт в счетчике пришедших заявок N (блок 4).

Последовательно сравниваем T_с в порядке приоритетов (блоки 5, 6, 7, 8) с временами освобождения T₁ канала 1, канала 2 — T₂, места в очереди 1 — T₃, места в очереди 2 — T₄. Как только обнаруживается факт того, что место в системе свободно (см. рис. 30.5): T_с > T₁, или T_с > T₂, или T_с > T₃, или T_с > T₄, так немедленно переводим заявку на свободное место и имитируем обработку ее на этом месте.

Рис. 32.5. Механизм определения освобождения канала

(иллюстрация)

Допустим, что освободилось место в первом канале. Обработка состоит в том, что вычисляется время простоя этого канала до прихода заявки (например, T_с – T₁), и это время прибавляется в счетчик времен простоя (блок 15). Вычисляется следующее время изменения состояния канала — модифицируется переменная T₁, которая укажет нам в дальнейшем, когда снова освободится канал. Величина T₁ изменяется на величину τ:= –1/μ₁ · Ln(r) — время обслуживания, отсчитываемую от начала обслуживания T_с. Счетчик обслуженных заявок N_об увеличивается на единицу.

Аналогично обработка происходит и во втором канале, если заявка попадет именно туда (блок 14).

Особенность обработки заявки в очереди состоит в том, что первое место в очереди освобождается, когда освобождается место в одном из каналов, конечно, заявка уходит туда, где место освобождается раньше (блоки 5, 6). Второе место в очереди освобождается одновременно с первым, так как заявка в очереди передвигается на первое освободившееся место (блок 12).

Далее алгоритм генерирует в цикле следующую заявку (блоки 3, 16). Остановка моделирования происходит тогда, когда каждая линейка будет заполнена до момента Tk (блок 16). После этого происходит обработка статистических результатов, накопленных в счетчиках (блок 17). Вероятность оценивается частостью появления события, которая вычисляется как отношение количества появившихся событий к количеству возможных таких появлений.

Блок-схема алгоритма показана на рис. 32.6.

Рис. 32.6. Блок-схема алгоритма, реализованного по принципу последовательной

проводки заявок. Пример — моделирование системы массового обслуживания

И, конечно, надо помнить, что чем больше время моделирования, тем точнее будет вычисленный результат.

Имеет смысл напомнить еще раз, что необходимо наблюдать за поведением статистической характеристики, какой, например, является P_об. Ранее (см. лекцию 21, лекцию 34) мы отмечали, что статистическая величина меняется в зависимости от времени наблюдения. Как только статистическая величина перестает меняться в пределах объявленной точности, то есть кривая входит в коридор, отведенный ей точностью, то это сигнализирует о достаточности количества экспериментов.

Необходимо внимательно следить, чтобы все искомые переменные вошли в интервал объявленной точности, только тогда можно прекратить моделирование и быть уверенным в результате.

Для повышения эффективности алгоритма (уменьшения времени его работы) можно отбросить нехарактерную часть реализации — обычно это начальный участок работы системы, «выход ее на режим».

Заметим также, что не важно, имеем ли мы дело с одной длинной реализацией или с большим количеством коротких реализаций (у которых, конечно, вырезан участок «выход на режим»), в сумме дающих реализацию такой же длины — статистический результат будет тем же. Это рассуждение устанавливает равенство усреднений по ансамблю реализаций усреднениям по времени.

Примечание. На практике обычно применяют комбинации всех трех методов.

Дата добавления: 2014-01-07