Приведение квадратичных форм к каноническому виду

Рассмотрим некоторое линейное преобразование 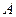с матрицей .

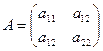Это симметрическое преобразование можно записать в виде:

,

,

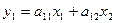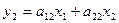где 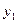и 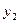– координаты вектора 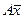в базисе .

Очевидно, что квадратичная форма может быть записана в виде

.

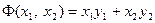Как видно, геометрический смысл числового значения квадратичной формы Ф в точке с координатам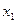и и 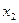– скалярное произведение .

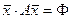Если взять другой ортонормированный базис на плоскости, то в нем квадратичная форма Ф будет выглядеть иначе, хотя ее числовое значение в каждой геометрической точке и не изменится. Если найти такой базис, в котором квадратичная форма не будет содержать координат в первой степени, а только координаты в квадрате, то квадратичную форму можно будет привести к каноническому виду.

Если в качестве базиса взять совокупность собственных векторов линейного преобразования, то в этом базисе матрица линейного преобразования имеет вид:

.

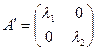При переходе к новому базису от переменных 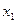и 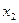мы переходим к переменным 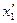и . Тогда:

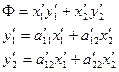
Тогда .

Выражение 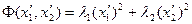называется каноническим видом квадратичной формы. Аналогично можно привести к каноническому виду квадратичную форму с большим числом переменных.

Теория квадратичных форм используется для приведения к каноническому виду уравнений кривых и поверхностей второго порядка.

Пример 9.1. Привести к каноническому виду квадратичную форму

.

Решение.

Коэффициенты: , , .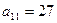

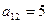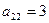Составим характеристическое уравнение: ;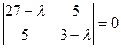

; ;

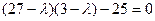
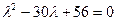
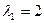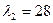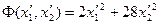
Пример 9.2. Привести к каноническому виду уравнение второго порядка:

.

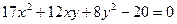Решение.

Коэффициенты , , .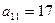

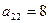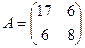
Составим характеристическое уравнение: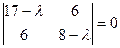

; ;

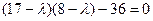
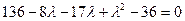
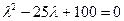
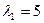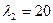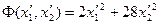
Итого: 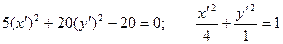– каноническое уравнение эллипса.

Пример 9.3. Используя теорию квадратичных форм, привести к каноническому виду уравнение линии второго порядка. Схематично изобразить график.

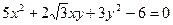
Решение: Составим характеристическое уравнение квадратичной формы 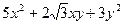: при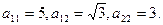

Решив это уравнение, получим ; .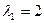

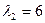Найдем координаты собственных векторов:

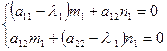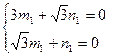, полагая 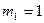, получим ;

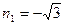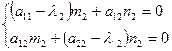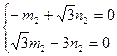, полагая 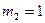, получим .

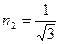Собственные векторы: .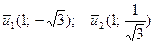

.

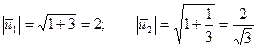Находим координаты единичных векторов нового базиса.

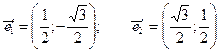
Имеем следующее уравнение линии в новой системе координат:

.

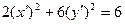Каноническое уравнение линии в новой системе координат будет иметь вид:

.

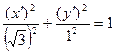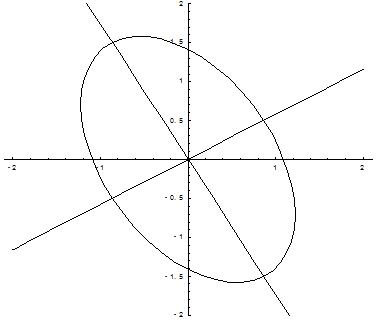
Рис. 9.1.

Пример 9.4. Используя теорию квадратичных форм, привести к каноническому виду уравнение линии второго порядка. Схематично изобразить график.

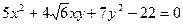
Решение: Составим характеристическое уравнение квадратичной формы 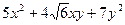: при

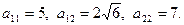
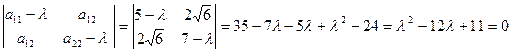
Решив это уравнение, получим .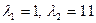

Найдем координаты собственных векторов:

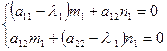, полагая 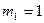, получим ;

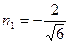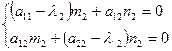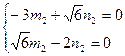, полагая 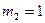, получим .

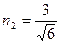Собственные векторы: .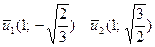

.

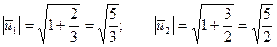Находим координаты единичных векторов нового базиса.

.

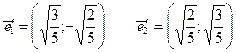Имеем следующее уравнение линии в новой системе координат:

.

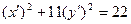Каноническое уравнение линии в новой системе координат будет иметь вид:

.

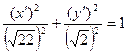Рис. 9.2.

Пример 9.5. Используя теорию квадратичных форм, привести к каноническому виду уравнение линии второго порядка. Схематично изобразить график.

Решение.

Коэффициенты: .

Характеристическое уравнение: .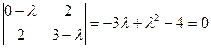

Корни:

Для : , , .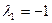

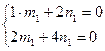
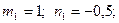
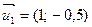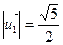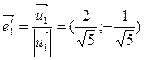Для : , , , .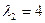

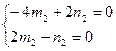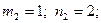
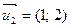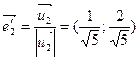Получаем: – каноническое уравнение гиперболы.

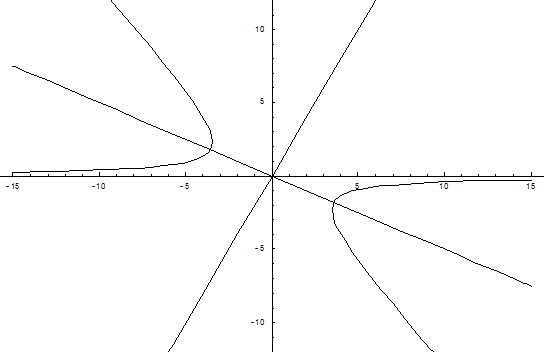
Рис. 9.3.

Дата добавления: 2014-01-07