Обратные матрицы

Параболический цилиндр

Гиперболический цилиндр

Мнимый эллиптический цилиндр

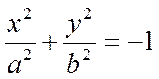
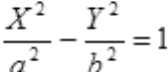
Y ² = 2 pX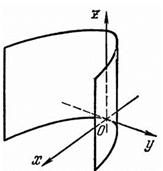

(Возвращение в линейную алгебру)

Пусть дана квадратная матрица А

aij – минор 1ого порядка

Mij – дополнительный минор порядка (n-1)

Aij=(-1) ∙Mij – алгебраическое дополнение для aij

Определитель 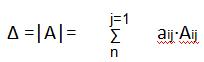(где i-фиксированно)

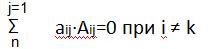
Матрица B называется обратной матрицей по отношению к A, если A*B=B*A=E(единичная матрица).

Замечание: Обратная матрица для квадратной матрицы В, имеет тот же порядок, что и исходная, если она существует.

Теорема:

Всякая невырожденная квадратная матрица любого порядка имеет обратную:

-ассоциированная матрица (присоединенная).

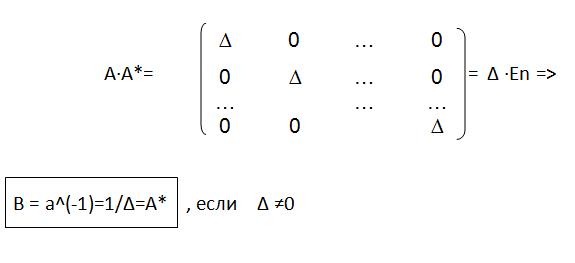
Вспомним,

1. a □ (b□c)=(a□b) □c

2. Ǝ z є V | ∀ a є V |a□z=z□a=a

3. ∀ a Ǝ n | n□a=a□n=z

4. a□b=b□a

5. (α+β) ∆ a=(α∆a)□(β∆a)

6. α∆ (a□b)= (α∆ a) □(α∆ b)

7. α∆ (β ∆ a)= (αβ)∆ a

8.1∆ a=a

∀ a, b є V; α,β є P; 1 є P

Система векторов, состоящая из хотя бы одного вектора:

1) A1=(ā)- линейно зависима ↔ ā =0

b=λ ā, так как ā =0, то b=0, значит A1=(ā) – линейно зависима

2) А1=(ā)-линейно независима ↔а≠0

По определению b=0;

b=λa, так как a≠0, то λ =0, значит A1=(a) – линейно независима.

3) А2=(ā1, ā2)-линейно зависима↔ ā1|| ā2, то вектор а линейно выражается через ā2, следовательно, по критерию линейной зависимости А2=(ā1, ā2) –линейно зависима.

4) А2=(ā1, ā2)-линейно-независима↔ ā1|| ā2

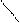ā1|| ā2→ ā1-линейно не выражается через ā2, значит А2-линейно-независима

Теорема: Определитель произведения двух квадратных матриц равен произведению их определителей.

|АВ|=|А|∙|В|

А=(aij), mxn

B=(bij),mxn

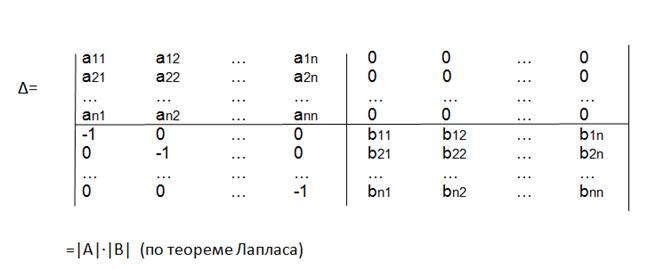
Преобразуем определитель так, чтобы в правом нижнем углу были «0»,но чтобы величина определителя не менялась.

S=(1+2+…+n)+(n+1+n+2+…+n+n)=2(1+2+n)+n∙n

(-1)^(n+s)=2n(n+1)+n+n^2=2n(n+1)

Теорема: «Необходимое условие существования матрицы»

Для того чтобы квадратная матрица А имела обратную матрицу, она не должна быть невырожденная.

Доказательство:

Пусть есть обратная матрица А^(-1)

A∙A^(-1)=A∙(-1) ∙A=E(по определению)

По предыдущей теореме переходим к:

|A|∙|A^(-1)|=|E|=1 → |A|≠0

Теорема: Пересечение двух подпространств является подпространством.

Дано: V-векторное пространство, L1, L2 є V

L1 подпространство пространства V Это означает:

1) ā1, ā2 є L → ā1 + ā2 є L1

2) ∀ числа λ и ∀ ā1 є L1 → λ∙ ā1 є L1

(замкнутость относительно линейных операций)

Доказательство:

Берем L1 ∩ L2 = L

1. ā1, ā2 є L → ā1, ā2 є L 1 и ā1, ā2 є L 2

→ ā1 + ā2 є L1 и ā1 + ā2 є L2 → ā1 + ā2 є L2 → ā1 + ā2 є L1→ ā1 + ā2 є L → L1 ∩ L2

2. ∀ числа λ и ∀ ā1 є L1

λ∙ ā1 є L1 и λ∙ ā1 є L1 → λ∙ ā1 є L

Дата добавления: 2014-01-07