Векторное пространство

Сумма двух подпространств.

V, lim V=n

L1, L2 є V

Подпространство L= L1+ L2 =(def)={ӯ1=ā1 + ā2 | ā1 є L 1, ā2 є L2 }

Доказательство:

ӯ1, ӯ2 є L1 + L2 ↔ ӯ1=ā1 + ā2 и ӯ2=ā3 + ā4

ā1, ā3 є L 1, ā2, ā4 є L2

1) ӯ1+ ӯ2= (ā1 + ā2) + (ā3 + ā4)= (ā1 + ā3) + (ā2 + ā4)

є L 1 є L2

2) ∀ числа λ и ∀ ӯ 1 є L | λ∙ ӯ= λ∙(ā1 + ā2)= λ∙ā1+ λ∙ ā2= L1 + L2

є L 1 є L2

Теорема о пополнение

Пусть V - векторное пространство dimV=n(∃ базис ē₁,ē₂, …,ē_n). ∀ линейно-независимую упорядоченную систему векторов (ƒ̅ ₁,ƒ̅₂, …, ƒ̅_n)⊂ V можно дополнить до некоторого базиса пространства V. В частности ∀ не нулевой вектор V можно включить в некоторый базис.

Если s=n, то это уже базис.

Если s>n быть не может, потому что в ∀ системе векторов больше, чем в базисе – она линейно зависима.

Если s<n:

(1) ƒ̅ ₁, ƒ̅₂, …, ƒ̅_s, ē₁, ē₂, …,ē_n – (n+s) векторов. Отбросим все векторы, которые выражаются через предыдущие. Так как F_s линейно независима, то она остается, по критерию линейно независимости.

(2) ƒ̅ ₁, ƒ̅₂, …, ƒ̅_s, ē _𝑖1, ē_𝑖2, …,ē_𝑖𝑛 составим произвольную линейную комбинацию

α₁ ƒ̅ ₁, α₂ ƒ̅₂, …, α_s ƒ̅_s, β₁ ē _𝑖1, β₂ ē_𝑖2, …, β_k ē_𝑖n

β_n с максимальным n, β_n ≠0 ⇒ ē_𝑖n выражается через предыдущий ⇒ β_n =0

α₁ ƒ̅ ₁+ α_s ƒ̅_s=ō ⇒ α₁,α₂,…,α_s =0

Значит, наша система 2 линейно независима.

2 – полная система, так как ∀ вектор пространства V линейно выражается через систему 1, через 2в силу транзетивности: линейный вектор пространства V выражается через систему 2.

Следствия:

Если есть подпространство пространства, то размерность подпространства не превосходит размерность пространства: L⊂V ⇒ dimL≤dimV

dimL=dimV ⇒ L=V

Базис любого подпространства можно включить в некоторый базис объемлющего пространства.

Сумма подпространств.

Сумма подпространств – это такое множество, которое состоит из элементов одного и другого подпространств

Теорема. Размерность суммы.

Пусть U и W –конечномерные подпространства V.

dim(U+W) = dimU + dimW - dimU∩W

k = dimU p=dimW m = dimU∩W

U∩W⊂U ⇒ m ≤ k

U∩W⊂W ⇒ m ≤ p

В пересечение подпространств выбираем какой либо базис

ē₁, ē₂, …,ē_m(базис U∩W) a̅₁, …, a̅_k-m-базис в U

ē₁, ē₂, …,ē_m(базис U∩W) b̅ ₁,…,b̅̅ _p-m базис в W

z = u + w u∊U,w∊W

u+w=[ ē₁, ē₂, …,ē_m, a̅₁, …, a̅_k-m, b̅ ₁,…,b̅̅ _p-m ] – линейная оболочка.

Любой вектор суммы принадлежит линейной оболочке.

Осталось проверить линейную независимость.

Равенство нулю возможно только в тривиальном случае.

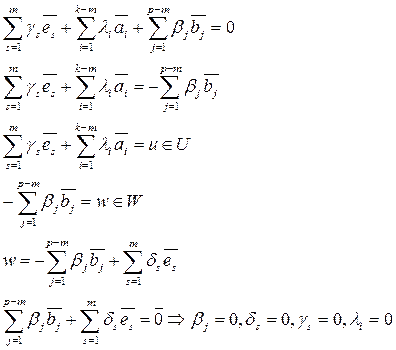
Дата добавления: 2014-01-07