Критерий базиса

Критерии базисов.

Внешняя прямая сумма.

Теорема.

Прямая сумма.

Определение.L₁ L₂ – Подпространства из V.

dim(L₁+L₂) = dimL₁ + dimL₂ – dim(L₁∩L₂)

L₁+L₂ – называется прямой суммой, если для любого вектора а̅ ∊ L₁+L₂ | а̅ ∊ = а̅₁ + а̅₂ однозначно, где а̅_𝑖 ∊ L_𝑖

Если L₁∩L₂ = {0}-дизъюнктные подпространства.

L₁+L₂ –Прямая сумма тогда, и только тогда, когда L₁ и L₂ - дизъюнктны.

Доказательство:

Пусть L₁+L₂ прямая сумма тогда, и только тогда, когда ∀а̅ ∊ L₁+L₂⃒ а̅ = а̅̅₁+а̅₂ ⃒b̅ ∊ L₁∩L₂ ∼ b̅∊ L₁, b̅∊ L₂⇒ а̅ = (а̅̅₁+ b̅) + (а̅̅₁- b̅) – однозначно (а̅_𝑖 ∊ L_𝑖)⇒ сумма прямая ⇔ пересечение нулевое.

Понятие как суммы, так прямой суммы, распределяются на любое число слагаемых.

L₁⊕L₂ – обозначение прямой суммы (внутренняя прямая сумма).

Пусть заданы два векторных пространства L₁ и L₂.

V = L₁𝗑 L₂ – декартого произведение.

𝒰,𝒱 ∊ V = L₁𝗑 L₂

𝒰 =(𝒰₁,𝒰₂) ⃒ 𝒰_𝑖∊ L_𝑖

𝒱=(𝒱₁,𝒱₂) ⃒ 𝒱_𝑖∊ L_𝑖

𝒰+𝒱=(𝒰₁,𝒰₂)+(𝒱₁,𝒱₂)≝(𝒰₁+𝒱₁,𝒰₂+𝒱₂).

∀ λ – число λV = λ(V₁,V₂)≝(λV₁,λV₂)

V₁={V=(V₁,0)∊V}≡ L₁𝗑{0} – пластина произведения L₁𝗑 L₂ параллельная L₁

V₂={V=(0,V₂)∊V}≡ L₂𝗑{0} – пластина произведения L₁𝗑 L₂ параллельная L₂

V₁ ≌ L₁, V₂ ≌ L₂ , V≌ L₁⊕L₂ – внешняя прямая сумма.

Пусть дано векторное пространство векторов V конечномерное

dimV = n

∀ dimV = n (∃ базис ē₁, ē₂, …,ē_n)

𝒜 _n=(𝑎̅₁,𝑎̅₂, …, 𝑎̅_n).

𝒜_n базис ⇔ 𝒜 линейно независима.

2 Критерий базиса.

𝒜_n базис ⇔ 𝒜_n полная система.

Доказательство: 𝒜_n линейно независима ∀𝑎̅∊V

𝒜_n+1=(𝑎₁,𝑎₂, …, 𝑎_n,𝑎̅) – линейно зависима.

𝒜_n+1 линейно зависима через базис.

n+1 ≥ n по теореме о линейной зависимости, что 𝑎_n+1 – линейно зависим ⇒

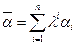
Если коэффициент при 𝑎не 0 то 𝑎выражается ⇒полная система.

Если коэффициент при 𝑎=0 то не существует 𝑎_n+1элементов ⇒противоречие.

Пусть 𝒜_n– полная.

∀𝑎̅ из V

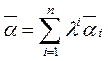
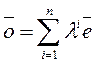
[e̅₁, e̅₂,…, e̅_n]=V

𝒜_n– полная [𝒜_n] = V

Отступление: Ранг системы векторов.

Пусть дано 𝒜_n.

Определение: Максимальное число линейно независимых векторов, называется её рангом, а векторы входящие в это число образуют ранговую подсистему.

𝒜_n– полная [𝒜_n] = V

r= rang𝒜_n= rang𝒜_r

𝒜_r⊂𝒜_n

𝒜_r- ранг подсистемы.

Справедливы следующие утверждения:

1) Любая система 𝒜_nлинейно выражается через любую свою ранговую подсистему.

2) Линейная оболочка совпадает с любой своей оболочкой подсистемы.

3) [𝒜_r] =[𝒜_n]

dim[𝒜_r] = dim[𝒜_n]=r

Дата добавления: 2014-01-07