Следствие

1) rang𝒜≤n

2) Так как 𝒜_∙n⊂R^m⇒rang𝒜≤ m

Мысленно перебераем миноры матрицы.

Рассмотрим миноры порядка k, 1 ≤ k≤ min(m,n)

Обязательно найдется ненулевой минор высшего порядка.

Он всегда существует для каждой фиксированной тматрицы.

Теорема о ранге матрицы.

Наивысший порядок отличных от нуля миноров матрицы равен рангу этой матрицы.

Замечание: Если все миноры порядка kравны нулю, то равны нулю и все миноры более старшего порядка(более высоких порядков, если они есть).

По теореме Лапласа: более высокий минор можно разложить по минорам наименьшего порядка.

Доказательство: Обозначим rнаивысший порядок миноров матрицы отличных от нуля.

Предположим, что некоторый минор стоит в левом верхнем углу(rпервых столбцов занимаем этот минор).

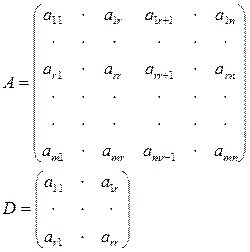
Если D≠0, то r– наивысший порядок отличный от нуля.

∆ i =0 при r≤i≤m, т.к. в этом случае ∆i – минор матрицы А порядка r+ 1 для любого i∆i =0⇒Мы приходим к выводу, что ∆i =0 ∀1≲ i ≲ m.

Каждый столбец с номером l ≥ r есть линейная комбинация первых rстолбцов.

Это означает, что первые rстолбцы образуют ранговую подсистему системы всех столбцов.

Мы рассмотрели случай, когда минор в левом верхнем углу. А если в другом месте? Общий случай сводиться к рассмотренному путем перемены местами строк и столбцов. Тогда наш минор всегда загониться в левый верхний угол.

При этом не ранг матрицы, не порчее не меняется.

Дата добавления: 2014-01-07