
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Метрические задачи
|
|
|
|
В прямоугольной декартовой системе координат можно решать все перечисленные выше аффинные задачи на взаимное расположение точек на прямой и плоскости, а также задачи на вычисление расстояний и углов – метрические.
Задача 10. Вычисление расстояния между двумя точками
Дано: 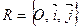 , М 1(х 1; у 1), М 2(х 2; у 2)
, М 1(х 1; у 1), М 2(х 2; у 2)
Найти: расстояние  .
.
 Решение. Расстояние между двумя точками М 1 и М 2 вычислим как длину отрезка М 1 М 2 (рис.1.13), равную длине (модулю, абсолютной величине) вектора
Решение. Расстояние между двумя точками М 1 и М 2 вычислим как длину отрезка М 1 М 2 (рис.1.13), равную длине (модулю, абсолютной величине) вектора 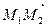 :
:
 .
.
 , значит,
, значит,
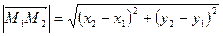 .
.
|
Тогда
 (13)
(13)
Расстояние между двумя точками плоскости равно квадратному корню из суммы квадратов разностей одноименных координат.
Пример 6.
Дано: М 1(6; 0), М 2(–2; 1).
Найти: расстояние М 1 М 2.
Решение.
 .
.
 .
.
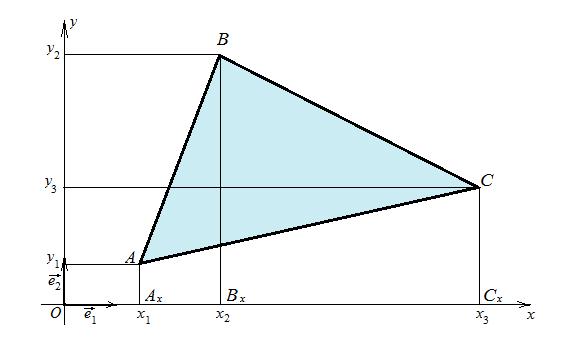
Задача 11. Вычисление площади треугольника
Дано:  , А (х 1; у 1), В (х 2; у 2), С (х 3; у 3).
, А (х 1; у 1), В (х 2; у 2), С (х 3; у 3).
Найти: площадь треугольника АВС.
Решение (рис.1.14).
|
 .
.
Вычислим площади трапеций АхВхВА, ВхСхСВ, АхСхСА по формуле 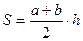 :
:
 ,
,
аналогично  ,
,  .
.
Тогда 


 .
.
Точки А, В и С могут располагаться иначе, а определитель, составленный из их координат – положительным или отрицательным числом, поэтому
 . (14)
. (14)
Если точки А, В и С лежат на одной прямой, то S =0 и, наоборот.
Пример 7.
Дано: А (6; 0), В (–2; 1), С (2; 7).
Найти:  .
.
Решение.
 .
.  .
.
Литература и задания практикума (по УМК):
| [2] | гл.1, §1 | № 9-14 |
| [10] | гл.1, §1 | № 1-25 |
| [2] | гл.1, §1 | № 15-25,37-39 |
| [10] | гл.1, §1 | № 41-61,73-85 |
2. Данко П.Е. Высшая математика в упражнениях и задачах: в 2-х частях: учеб. пособие / П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова. – М.: Высшая школа, 1998. – Ч.1.
8. Сборник задач для самостоятельной работы по геометрии / авт.-сост. Т.М. Соромотина. – 2-е изд. – Пермь: Изд-во ПГПУ, 2008.
10. Цубербиллер О.Н. Сборник задач и упражнений по аналитической геометрии / О.Н. Цубербиллер. – 32-е изд. – СПб.: Лань, 2005.
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 271; Нарушение авторских прав?; Мы поможем в написании вашей работы!