
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Принцип линейной частотной модуляции (ЛЧМ)
|
|
|
|
Сигналы с внутриимпульсной частотной модуляцией
Лекция №10
- Принцип линейной частотной модуляции
- Спектр прямоугольного ЛЧМ-импульса
- ЛЧМ-сигналы с большой базой
- Авокорреляционная функция ЛЧМ-сигнала.
Использование пассивной радиолокации позволяет обнаруживать объекты, классифицировать их и принимать соответствующие решения, например, по управлению воздушным движением и т.д. Дальность действия радиолокационной станции (РЛС) зависит от многих факторов: мощности передатчика, чувствительности приемника, типа антенны и т.д. Однако в современных РЛС технические возможности по вышеуказанным причинам практически исчерпаны. Принципиально повысить дальность обнаружения объекта позволяет использование сигналов с внутриимпульсной частотной модуляцией.
В настоящей лекции будут [8-12] рассмотрены спектральные и корреляционные свойства особого класса модулированных сигналов, получивших в последнее время широкое распространение в радиолокации. Эти сигналы отличаются от обычных радиоимпульсов тем, что их высокочастотное заполнение имеет переменную частоту. Чаще всего используется внутриимпульсная частотная модуляция с линейным законом изменения мгновенной частоты во времени.
Рассмотрим радиоимпульс с огибающей прямоугольной формы. Принципиально импульс может быть любой формы, однако наиболее просто можно получить импульс именно прямоугольной формы. Рассмотрим наиболее простую задачу и будем полагать, что частота заполнения линейно нарастает от начала импульса к его концу. Конкретизируя математическую модель сигнала, предположим, что его длительность равна tи, причем точка t = 0 соответствует середине импульса, а мгновенная частота изменяется во времени по закону
 (1)
(1)
Здесь ω0 — несущая частота; μ — параметр с размерностью с-2, равный скорости изменения частоты во времени. Легко видеть, что за время, равное длительности импульса девиация частоты
 (2)
(2)
Полная фаза сигнала
 (3)
(3)
Итак, будем называть радиоимпульсом с линейной частотной модуляцией, или ЛЧМ- имульсом, сигнал, представляемый следующей математической моделью:
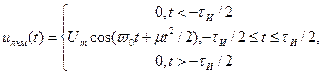
 (4)
(4)
Замечательное свойство ЛЧМ-сигналов, определяющее их практическую значимость, состоит в следующем. Предположим, что имеется некоторое физическое устройство, осуществляющее задержку сигналов, подаваемых на его вход. Если время задержки зависит от частоты сигнала, причем с ростом частоты это время уменьшается, то при определенных условиях, подавая на вход такого устройства ЛЧМ-импульс большой длительности, можно добиться существенного «сжатия» его во времени. Этот эффект обусловлен чем, что на выходе устройства задержки одновременно будут появляться составляющие как более низкочастотные, относящиеся к началу импульса, так и более высокочастотные, наблюдаемые в его конце.
Подробный анализ устройств сжатия, позволяющих оценить количественную сторону явления, а также выяснить, например, форму выходного сигнала, будет проведен в последующем материале при обсуждении методов оптимального выделения сигналов на фоне помех.
Иногда для моделирования огибающей сигнала используют полиномы Чебышева:
Свойства полиномов Чебышева
Тригонометрической выражение.
 (4.1)
(4.1)
представляет собой полином степени m и называется полиномом Чебышева. Правая часть(4.1) определена на всей оси х, однако в расчетах чаще используются две записи
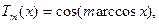 -1
-1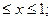 (4.2)
(4.2)
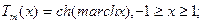 (4.3)
(4.3)
справедливые в различных областях. Степенной полином  на интервале[-1,+1] имеет m нулей,
на интервале[-1,+1] имеет m нулей,
 откуда следует
откуда следует
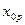 = cos
= cos  p=1,2,3…,m. (4.4)
p=1,2,3…,m. (4.4)
Если для упрощения полагать u = arccos x, то первые несколько полиномов имеют следующий:

Общее выражение для полинома Чебышева может быть представлено формулой
 (4.5)
(4.5)
где ( )целое число, ближайшее к m/2. Выражение (4.5) удовлетворяет рекуррентному соотношению
)целое число, ближайшее к m/2. Выражение (4.5) удовлетворяет рекуррентному соотношению
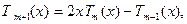 (4.6)позволяющему определить любой полином
(4.6)позволяющему определить любой полином  , если известны
, если известны  и
и  .Графики функции
.Графики функции  при m = 0, 1, 2, 3, 4 представлены на рис. 1.Полиномы Чебышева обладают следующими замечательными свойствами:- в пределах —1
при m = 0, 1, 2, 3, 4 представлены на рис. 1.Полиномы Чебышева обладают следующими замечательными свойствами:- в пределах —1 х
х  1 из всех полиномов данной степени с действительными коэффициентами и коэффициентами при старшем члене, равном 2
1 из всех полиномов данной степени с действительными коэффициентами и коэффициентами при старшем члене, равном 2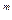 -1, имеют наименьшее максимальное значение, не превосходящее единицы;- имеют наибольшее значение наибольшего корня x
-1, имеют наименьшее максимальное значение, не превосходящее единицы;- имеют наибольшее значение наибольшего корня x
 |
т.е. интервал \Х
 ,1 \ является наименьшим;
,1 \ является наименьшим;
- при |х|> 1 они возрастают с наибольшей скоростью
Вопросы:
1.Детерминированные и стохастические сигналы, к какому классу относятся ЛЧМ сигналы?
2.Как можно увеличить дальность обнаружения РЛС?
3.Как добиться одновременного выхода низко и высокочастотных составляющих ЛЧМ сигнала?
4.Как аналитически можно представить электрический сигнал?
5. Какие эффекты можно наблюдать при другой аналитической зависимости, когда частота зависит от времени не по линейному закону?
2.Спектр прямоугольного ЛЧМ-нмпульса.
Как известно спектральный анализ является мощным оружием для анализа сигналов т.к. позволяет анализировать его спектр, анализировать взаимное влияние отдельных спектральных составляющих и т.д. В предыдущей лекции при рассмотрении спектральных характеристик ЧМ-сигнала, промодулированного двумя колебаниями низкой частоты, было показано, что спектр такого сигнала имеет сложную структуру из-за перекрестного влияния отдельных спектральных составляющих. Все это в полной мере относится и к спектру ЛЧМ-импульса. При дальнейшем изложении этого вопроса будем придерживаться в основном обозначений, принятых ранее.
На основании модели (4) запишем выражение спектральной плотности одиночного ЛЧМ-импульса. Для этого математическая модель исследуется на различных участках. И после соответствующих преобразований можно получить:
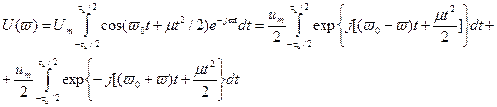 (5)
(5)
Анализ этого соотношения показывает, что первый интеграл описывает часть спектральной плотности с резко выраженным максимумом в области положительных частот, близких к ω0. Второй интеграл соответствует части спектральной плотности, сосредоточенной в основном при ω< 0. На практике интересуются исключительно случаем, когда эффект перекрытия спектров, концентрирующихся при положительных и отрицательных частотах, пренебрежимо мал. Это связано с тем, что полная девиация частоты за время длительности импульса очень мала по сравнению с несущей частотой:
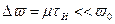
Поэтому в формуле (5) следует вычислять только первый интеграл, дающий спектральную плотность при ω >0.
С учетом сказанного, дополнив аргумент экспоненциальной функции в формуле (5) до полного квадрата, получим
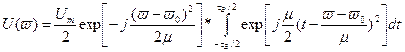 (6)
(6)
Для дальнейшего преобразования формулы 6 более удобно перейти от переменной t к новому аргументу х, выполнив замену переменной:
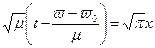
После замены переменной, проводя вычисления, после соответствующих преобразований находим:
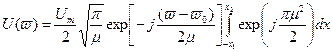 (7)
(7)
где пределы интегрирования определяются следующим образом:
 ;
;  (8)
(8)
Интеграл в выражении (7) сводится к комбинации хорошо изученных специальных функций — интегралов Френеля:
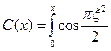 ;
; 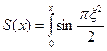
В результате получаем окончательную формулу для спектральной плотности ЛЧМ-сигнала:
 (9)
(9)
Представив эту спектральную плотность в показательной форме:
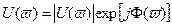
можно заметить, что модуль (амплитудный спектр)
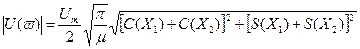 (10)
(10)
в то время как фазовый спектр состоит из квадратичного слагаемого
 (11)
(11)
и так называемого остаточного фазового члена
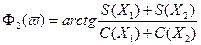 (12)
(12)
Вопросы:
1.Зачем проводится спектральный анализ сигнала и какую информацию можно извлечь из этого анализа?
2.Какова полная девиация частоты за время длительности импульса по сравнению с несущей частотой?
3.Использование, каких специальных функций облегчает математические выкладки?
4.Из каких частей состоит амплитудный спектр?
|
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 7768; Нарушение авторских прав?; Мы поможем в написании вашей работы!