Методы финансовых вычислений

2.1. Понятие простого и сложного процента

Предоставляя свои денежные средства в долг, их владелец получает определенный доход в виде процентов, начисляемых по некоторому алгоритму в течение определенного промежутка времени. Поскольку стандартным временным интервалом в финансовых операциях является 1 год, то наиболее распространен вариант, когда процентная ставка устанавливается в виде годовой ставки, подразумевающей однократное начисление процентов по истечении года после получения ссуды. Таким образом, процент выступает как причина изменения стоимости денег во времени.

Относительно момента выплаты или начисления дохода за пользование представленными денежными средствами проценты подразделяются на обычные и авансовые.

Обычные (декурсивные, postnumerando) проценты начисляются в конце периода относительно исходной величины средств. Доход на процент выплачивается в конце периодов финансовой операции. Такие операции обычно проводят в большинстве депозитных и кредитных операциях, а также в страховании.

Если же доход, определяемый процентом, выплачивается в момент предоставления кредита, то данная форма расчетов называется авансовой, или учетом, а применяемые проценты – авансовыми (антисипативными, prenumerando), которые начисляются в начале периода относительно конечной суммы денег. Доход на процент выплачивается в начале периода, в момент предоставления долга. Так рассчитываются проценты в некоторых видах кредитования, например при продаже товаров в кредит, в международных расчетах, в операциях с дисконтными ценными бумагами. При этом базой для расчета процентов служит сумма денег с процентами (сумма погашения долга), а исчисленные таким образом проценты взимаются вперед и являются авансом.

Известны две основные схемы дискретного начисления:

• схема простых процентов;

• схема сложных процентов.

При использовании простых процентов сумма обязательств начисляется на первоначальную сумму.

FV=PV(1+t·r), где

PV - настоящая стоимость капитала предназначенного для наращения

FV – будущая стоимость капитала, с учетом начисленных процентов

t – период начисления процентов

r – ставка процентов за период, выраженная в коэффициенте

Однако следует отметить, что такого рода вычисления встречаются крайне редко и чаще используют модифицированный вид данной формулы для начисления платежей для более мелких периодов времени.

FV=PV(1+t/Y·r), где

t – например (дни, месяцы)

Y – продолжительность года в днях

База для начисления сложных процентов постоянно меняется за счет присоединения ранее начисленных процентов.

FV=PV(1+r)^t, где

PV - настоящая стоимость капитала предназначенного для наращения

FV – будущая стоимость капитала, с учетом начисленных процентов

t – период начисления процентов

r – ставка процентов за период, выраженная в коэффициенте

Наращенная сумма при внутригодовой капитализации определяется по формуле:

FV=PV(1+n/r)^n·t/Y, где

t – например (дни, месяцы)

Y – продолжительность года в днях

n – количество раз начисления процентов за период Y

Пример 1. Рассчитать наращенную сумму с исходной суммы в 500 тыс.руб при размещении ее в банке на условиях начисления простых и сложных процентов, если: а) годовая ставка 20%; б) периоды наращения: 90 дней, 180 дней, 360 дней, 5 лет, 10 лет. Полагать, что в году 360 дней.

Расчет по простым процентам:

90 дней FV=PV(1+t·r) = 500 (1+90/360*0,2)=525

180 дней FV= 500 (1+180/360*0,2)=550

270 дней FV=500 (1+270/360*0,2)=575

360 дней FV=500 (1+360/360*0,2)=600

5 лет FV=500 (1+5*0,2)=1000

10 лет FV=500 (1+10*0,2)=1500

Расчет по сложным процентам:

90 дней FV= PV(1+r)^t = 500 (1+0,2)^90/360=500 1,2^1/4=523,3176

180 дней FV= 500 (1+0,2)^180/360=500 1,2^1/2=547,7226

270 дней FV=500 (1+0,2)^270/360=500 1,2^3/4=573,2657

360 дней FV=500 (1+0,2)^360/360=500 1,2¹=600

5 лет FV=500 (1+0,2)⁵=500 1,2⁵=1244,16

10 лет FV=500 (1+0,2)¹⁰=500 1,2¹⁰=3095,8682

(II) Начисления по сложным процентам

(I) Начисления по простым процентам

FV

PV

1 2 периоды

Рис.1 Простая и сложная схемы наращения капитала

Проведенные расчеты показывают, что при начислении простых процентов по истечении 10 лет исходная сумма вырастет в три раза, а при начислении сложных процентов более чем в 6 раз.

Графически взаимосвязь между простой и сложной схемой наращения капитала представлена на рис.1. Таким образом, в случае ежегодного начисления процентов для лица. предоставляющего кредит:

• более выгодной является схема простых процентов, если срок ссуды менее одного года (проценты начисляются однократно в конце периода);

• более выгодной является схема сложных процентов, если срок ссуды превышает один год (проценты начисляются ежегодно);

• обе схемы дают одинаковые результаты при продолжительности периода 1 год и однократном начислении процентов.

Прежде, чем рассматривать примеры финансовых вычислений, отметим, что общий (Y) и частный (t) периоды начисления процентов в днях могут быть выражены точно или приближенно, на практике встречаются следующие способы расчетов:

1) t и Y, измерены точно – это значит начислить точные проценты с фактическим сроком операции. Для определения t здесь пользуются специальной таблицей порядковых номеров дней в году: из номера окончания операции вычитают день ее начала (если день выдачи и день погашения ссуды считаются за 1).

2) Если t измерено точно, а Y - приближенно. Этот способ используется для вычисления обыкновенных (коммерческих) процентов с фактическим сроком операции. Поскольку при вычислении знаменатель больше, чем при расчетах в случае 1, т.е. 360, то размер начисленных процентов при прочих равных условиях также будет несколько большим: на 1,38889%. В России по такому принципу ведутся все банковские операции;

3) Когда t и Y измерены приближенно. Этот способ применяется для вычисления обыкновенных коммерческих процентов с приближенным сроком операции, при некоторых видах расчетов с населением.

Таблица 1.

Показатели вычисления периодов за год

Измерение	t	Y
Точное	Фактически дней в месяце (январь-31; Февраль – 28 или 29 Март -31	Фактически дней в году (365 или 366)
приближенное	Число дней в любом месяце принимается за 30 дней	Продолжительность года 360 дней

Пример 2. Предприятие получило ссуду 100 млн.руб. под 25% годовых с 01.04 по 01.07. Определить подлежащую возврату сумму. Долг гасится единовременным платежом.

Определим период погашения ссуды. Первое апреля не считаем, так как этот день является днем выдачи, а день погашения принимаем за 1 день, тогда:

t=30+31+30-1=90

FV=PV(1+t/Y·r)=100(1+90/360·0,25)=106,25

Пример 3. Доллары США, купленные по курсу 30 руб. за 1 долл., продали спустя 3 месяца по курсу 32 руб. за 1 долл. Исчислить доходность операции.

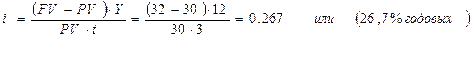
Дата добавления: 2014-01-07