Операции наращения и дисконтирования

Логика построения основных алгоритмов по решению инвестиционных задач достаточно проста и основана на следующей идее. Простейшим видом финансовой сделки является однократное предоставление в долг некоторой суммы РV с условием, что через некоторое время t будет возвращена большая сумма FV. Как известно, результативность подобной сделки может быть охарактеризована двояко: либо с помощью абсолютного показателя - прироста (FV – PV), либо путем расчета некоторого относительного показателя. Абсолютные показатели чаще всего не подходят для подобной оценки ввиду их несопоставимости в пространственно-временном аспекте. Поэтому пользуются специальным коэффициентом - ставкой. Этот показатель рассчитывается как отношение приращения исходной суммы к базовой величине, и качестве которой, очевидно, можно взять либо PV, либо FV. Таким образом, ставка рассчитывается по одной из двух формул:

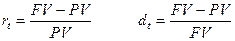
В финансовых вычислениях первый показатель имеет еще названия "процентная ставка", а второй - "учетная ставка", "дисконтная ставка". Оба показателя могут выражаться либо в долях единицы, либо в процентах. Различие в этих формулах состоит в том, какая величина берется за базу сравнения.

Как же соотносятся между собой эти показатели? Очевидно, что r_t>d_t, а степень расхождения зависит от уровня процентных ставок, имеющих место в конкретный момент времени. Так, если r_t = 8%, а d_t = 7,4%, то расхождение сравнительно невелико; если r_t = 80%, то d_t = 44,4%, т.е. ставки существенно различаются по величине.

В прогнозных расчетах (например, при оценке инвестиционных проектов), обычно имеют дело с процентной ставкой. Как правило, расчеты проводится в относительно стабильной экономике, когда уровни процентных ставок невелики и сравнительно предсказуемы в том смысле, что их значения не могут измениться в несколько раз. Если вероятна значительная вариабельность процентных ставок, должны применяться другие методы анализа и принятия решений, основанные главным образом на неформализованных критериях.

Процесс, в котором заданы исходная сумма и ставка, в финансовых вычислениях называется процессом наращения, искомая величина - наращенной суммой, а используемая в операции ставка - ставкой наращения. Процесс, в котором заданы ожидаемая в будущем к получению (возвращаемая) сумма и ставка, называется процессом дисконтирования, искомая величина - приведенной суммой, а используемая в операции ставка - ставкой дисконтирования. В первом случае речь о движении денежного потока от настоящего к будущему, во втором – о движении от будущего к настоящему.

Пример 4. Предприятие получило кредит на один год в размере 500 тыс.руб с условием возврата 1000 тыс. руб. В этом случае процентная ставка равна 100%, а дисконт - 50%:

В практике финансово-экономических расчетов часто требует определить будущую стоимость размещенных средств, но и решать обратную задачу: по сумме будущих размещенных средств определять требуемые суммы вложений, то есть осуществлять процесс дисконтирования.

В этих расчетах величина РV называется приведенной современной стоимостью суммы РV, а при операции наращения сумма FV выступает как будущая стоимость величины РV.

Следует иметь в виду, что привести стоимость денег можно к любому нужному моменту времени, а не обязательно к началу финансовой операции. Кроме того, с помощью дисконтирования определяют современную стоимость денег независимо от того, действительно ли совершалась кредитная операция и можно ли считать дисконтируемую сумму буквально наращенной.

Из формул наращения процентов производится обратное действие, или расчет денежных средств, предоставляемых в долг (величины РV). Такой способ начисления дохода называется математическим дисконтированием.

На практике подобные расчеты встречаются не часто. Например, для определения суммы капитала, которую нужно инвестировать под определенные проценты, чтобы получить требуемую сумму денег, а также чтобы начислить проценты, удерживаемые вперед при выдаче ссуды.

Пример 5. Ставка размещения краткосрочных денежных ресурсов для банков на 3 суток составляет 28% годовых. Какой объем средств необходимо разместить, чтобы в результате операции поступило 1,5 млн руб. (точные проценты).

Пример 6. Подлежащая возврату сумма долга — 10 млн руб. Определить сумму начисленных процентов, если срок ссуды 1 год, декурсивная ставка процентов 30% годовых.

Наиболее часто при анализе эффективности инвестиционных проектов проводят расчеты по дисконтированию с использованием сложной ставки процентов:

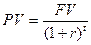
Пример 7. Определим сколько необходимо вложить денег в проект, будущая стоимость которого через 10 лет составит 200 млн.руб. Ставка дисконтирования за период составит 20%.

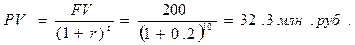
Пример 8. Ежегодно в конце года в течении 4 лет на счет поступают 50 тыс.руб. Определим будущую стоимость, если ежегодно в конце года осуществляется начисление сложных процентов при ставке 10%.

Наращенные отдельные платежи представляют геометрическую прогрессию. Тогда будущую стоимость можно определить по формуле:

Если вложения осуществляются чаще или реже, чем один раз в год, то формула модернизируется следующим образом:

n – количество платежей в год

j – ставка процентов

m – количество раз начисления процентов

Пример 9. Для погашения задолженности единовременным платежом через два года должником в кредитном учреждении создается погасительный фонд, в котором постепенно накапливаются достаточные для этого средства. Определим размер равных взносов в конце полугодия для создания через три года погасительного фонда в размере 500 млн.руб. Проценты на созданный фонд начисляются ежеквартально исходя из годовой ставки 26%.

Дата добавления: 2014-01-07