Критерии оценки систем

Оценка сложных систем в условиях неопределенности

При рассмотрении вопроса о критериях оценки систем основное внимание будет уделено оценке эффективности функционирования организационно-технических систем, где одним из звеньев является лицо, принимающее решение (ЛПР): решение, как правило, принимается в условиях неопределенности.

Рассмотрим систему А, состоящую из i подсистем (i изменяется от 1 до m).

Условия оценки эффективности функционирования систем для неопределенных операций можно представить в виде табл.10.1, в которой обозначены:

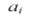- вектор управляемых параметров, определяющий свойства системы, состоящей из подсистем (i = 1,…,m);
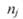- вектор неуправляемых параметров, характеризующий состояние внешней среды (j=1,…,k);
- значение эффективности i- подсистемы для n_j - состояния внешней среды;
- эффективность подсистемы a_i для всех состояний внешней среды.

Таблица 10.1 Оценка эффективности функционирования организационно-технической системы

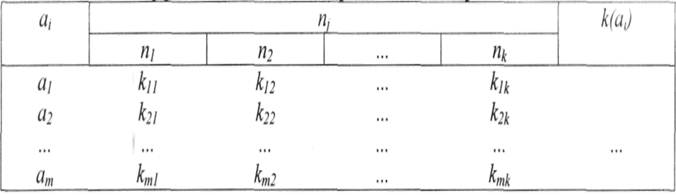
Каждая строка таблицы содержит значения коэффициента эффективности одной подсистемы для всех состояний внешней среды, а каждый столбец - значения эффективности для всех подсистемпри одном и том же состоянии внешней среды.

В случае задания состояний внешней среды одним параметром матрица коэффициентов эффективности может быть представлена диаграммой (рис. 10.1).

В неопределенной операции могут быть известны множество состояний обстановки и эффективность систем для каждой из них, но нет данных, с какой вероятностью может появиться то или иное состояние.

В зависимости от характера неопределенности операции могут делиться на игровые и статистически неопределенные. В игровых операциях неопределенность вносит своими сознательными действиями противник. Для исследования игровых операций используется теория игр. Условия статистически неопределенных операций зависят от объективной действительности, называемой природой.

Рис.10.1 Диаграмма эффективности подсистем a_i для условий n_j

В зависимости от характера предпочтений ЛПР наиболее часто в операциях, осуществляемых в условиях неопределенности, используются критерии:
• среднего выигрыша;
• Лапласа;
• Вальда (осторожного наблюдателя - максимина);
• максимакса;
• Гурвица (критерий пессимизма-оптимизма);
• Сэвиджа (критерий минимального риска).
Рассмотрим эти критерии на примере.

Пример. Необходимо оценить один из трех разрабатываемых программных продуктов а, для борьбы с одним из четырех типов программных воздействий K_j.

/ Матрица коэффициентов эффективности представлена в табл. 10.2.

Здесь a_{i -} программный продукт, i={1,2,3},

k_ij - оценка эффективности применения i -го программного продукта при j-м программном воздействии.
Критерий среднего выигрыша

Таблица 10.2

	Воздействие	К(аi)
КJ
К1	К2	К3	К4
Состояния (подсистемы)	а1	К11=0,1	К12=0,5	К13=0,1	К14=0,2	К (а1)=0,21
а2	К21=0,2	К22=0,3	К23=0,2	К24=0,4	К (а2)=0,28
а3	К31=0,1	К32=0,4	К33=0,4	К34=0,3	К (а3)=0,25
Вероятности	Р1=0,4	Р2=0,2	Р3=0,1	Р4=0,3

К (а₁) = Р₁ К₁₁ + Р₂ К₁₂ + Р₃ К₁₃ + Р₄ К₁₄ = 0,4 х 0,1 + 0,2 х 0,5 + 0,1 х 0,1 + 0,3 х 0,2 =

= 0,21

К (а₂) = 0,28

К (а₃) = 0,25

₄

К(а_i) = ∑ Pj Кij

_{j =1}

K_opt = max { K(a_i)}= max{ К (а₁) =0,21; К (а₂) = 0,28; К (а₃) = 0,25} = 0,28

_i

Критерий Лапласа

Таблица 10.3

	Воздействие	К(аi)
КJ
К1	К2	К3	К4
Состояния (подсистемы)	а1	К11=0,1	К12=0,5	К13=0,1	К14=0,2	К (а1)=0,225
а2	К21=0,2	К22=0,3	К23=0,2	К24=0,4	К (а2)=0,275
а3	К31=0,1	К32=0,4	К33=0,4	К34=0,3	К (а3)=0,3
Вероятности	Р1=0,25	Р2=0,25	Р3=0,25	Р4=0,25

Р₁ = Р₂ = Р₃ = Р₄ = 0,25 Равные вероятности

К (а₁) = 0,25 ∑ К₁j = 0,225

К (а₂) = 0,25 ∑ К₂j = 0,275

К (а₃) = 0,25 ∑ К₃j = 0,3

K_opt = max { K(a_i)}= max {К (а₁) =0,225;К (а₂)=0,275; К (а₃)=0,3} = 0,3

_i

Критерий Вальда (осторожного наблюдателя - максимина)

Дата добавления: 2014-01-07