Статистическое математическое ожидание

ТМ к лекции № 11

Точечные и интервальные оценки статистических числовых характеристик

Статистическая оценка математического ожидания, построенная для первичного статистического ряда имеет вид

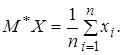(1)

Для вариационного ряда оценка имеет вид

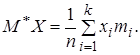(2)

Оценку (1) и (2) можно рассматривать как среднее значение из n значений данной выборки. Но можно считать, что имеем среднее из n значений различных независимых случайных величин X_i, распределенных по одному и тому же закону. Пусть MX_i=m и DX_i=s². Тогда

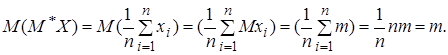
Это значит, что оценка (1) является несмещенной, и, пользуясь ею, мы допускаем только случайную ошибку, вызванную действием случайных факторов.

По следствию из закона больших чисел

Это значит, что оценка (1) является состоятельной.

Можно показать, что для нормальной случайной величины она является эффективной. В остальных случаях она приближается к эффективной при n®¥.

Дата добавления: 2014-01-07